题目内容
 要用总长为20m的铁栏杆,两面靠墙,围成一个矩形的花圃,怎样围法,才能使围成的花圃面积最大?
要用总长为20m的铁栏杆,两面靠墙,围成一个矩形的花圃,怎样围法,才能使围成的花圃面积最大?考点:二次函数的应用
专题:
分析:设矩形靠墙一面的长为xm,则两端的长为(20-x)÷2m,根据矩形面积公式求面积表达式,再根据性质求最值.
解答:解:设矩形靠墙的一面长为xm,面积为sm2
根据题意得s=x×
=-
x2+10x=-
(x-10)2+50,
∵-
<0,
∴函数有最大值,
当x=10时,s最大.
此时矩形两端长为5m.所以当两端各长5m,与墙平行的一边长10m时围成的花圃的面积最大.
根据题意得s=x×
| 20-x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵-
| 1 |
| 2 |
∴函数有最大值,
当x=10时,s最大.
此时矩形两端长为5m.所以当两端各长5m,与墙平行的一边长10m时围成的花圃的面积最大.
点评:此题考查了二次函数的应用,关键是得出面积的表达式,将实际问题转化为函数问题解答,渗透了数学建模的思想.

练习册系列答案
相关题目
下列计算正确的是( )
| A、-4+3=1 |
| B、|-5|=-5 |
| C、2×(-2)=-4 |
| D、90-8=1 |
 在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据
在四边形ABCD中,∠A=60°,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD,BC的长(精确到1米,参考数据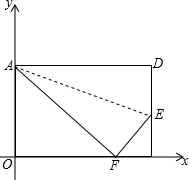 折叠矩形ABCD的一边AD,折痕为AE,且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系.求点F和点E坐标.
折叠矩形ABCD的一边AD,折痕为AE,且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系.求点F和点E坐标.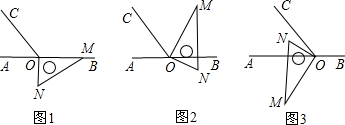
 如图,在3×3的方格纸中,每个小方格都是边长为1的正方形,O,A,B是格点,求
如图,在3×3的方格纸中,每个小方格都是边长为1的正方形,O,A,B是格点,求
 如图,分别以正方形四边中点为圆心作四段圆弧(在正方形内相交),剪去黑色部分,就可得到一朵窗花,已知正方形的边长为10,求一朵窗花的面积.
如图,分别以正方形四边中点为圆心作四段圆弧(在正方形内相交),剪去黑色部分,就可得到一朵窗花,已知正方形的边长为10,求一朵窗花的面积. 如图,∠AOB=90°,直线CD将∠AOB分成2:3两部分,∠AOC大于∠BOC,那么∠BOC=
如图,∠AOB=90°,直线CD将∠AOB分成2:3两部分,∠AOC大于∠BOC,那么∠BOC=