题目内容
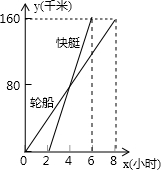如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象．根据图象下列结论错误的是（ ）| A、轮船的速度为20km/h |
| B、快艇的速度为40km/h |
| C、轮船比快艇先出发2h |
| D、快艇不能赶上轮船 |
考点：一次函数的应用
专题：
分析：由函数图象提供的数据信息根据行程问题的数量关系：速度=路程÷时间就可以得出结论．
解答：解：由函数图象，得
A、轮船的速度为：160÷8=20km/h，故A正确，
B、快艇的速度为：160÷（6-2）=40km/h，故B正确，
C、由函数图象可以得出轮船比快艇先出发2h，故C正确，
D、设快艇出发x小时后追上轮船，由图象，得
40x=20（x+2），
x=2，
则快艇出发2小时后与轮船相遇，故D错误．
故选D．
A、轮船的速度为：160÷8=20km/h，故A正确，
B、快艇的速度为：160÷（6-2）=40km/h，故B正确，
C、由函数图象可以得出轮船比快艇先出发2h，故C正确，
D、设快艇出发x小时后追上轮船，由图象，得
40x=20（x+2），
x=2，
则快艇出发2小时后与轮船相遇，故D错误．
故选D．
点评：本题考查了一次函数的图象的运用，行程问题的数量关系的运用，解答时分析清楚函数图象提供的信息是关键．
练习册系列答案
相关题目
如图，在一幅长为60cm，宽为40cm的矩形风景画的四周镶一条相同宽度的纸边，制成一幅矩形挂图．若要使整个挂图的面积是3500cm2，设纸边的宽为x（cm），则x满足的方程是（ ）| A、（60+x）（40+x）=3500 |
| B、（60+2x）（40+2x）=3500 |
| C、（60-x）（40-x）=3500 |
| D、（60-2x）（40-2x）=3500 |
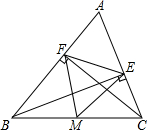如图，在△ABC中，CF⊥AB于点F，BE⊥AC于点E，M为BC的中点．
如图，OA，OB是⊙O的半径，C是⊙O上的一点，∠AOB=40°，∠OCB=50°，求∠OAC的度数．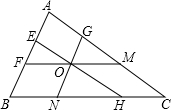
已知O是△ABC内一点，且GN∥AB，FM∥BC，EH∥AC，求证：
已知在△ABC中，∠B=∠C，BD=CE，求证：DE∥BC．