题目内容
如图，OA，OB是⊙O的半径，C是⊙O上的一点，∠AOB=40°，∠OCB=50°，求∠OAC的度数．考点：圆周角定理,垂径定理
专题：
分析：先根据圆周角定理求出∠ACB的度数，进而得出∠ACO的度数，由等腰三角形的性质即可得出结论．
解答：解：∵∠AOB=40°，
∴∠ACB=
×40°=20°．
∵∠OCB=50°，
∴∠ACO=50°-20°=30°．
∵OA=OC，
∴∠OAC=∠ACO=30°．
∴∠ACB=
| 1 |
| 2 |
∵∠OCB=50°，
∴∠ACO=50°-20°=30°．
∵OA=OC，
∴∠OAC=∠ACO=30°．
点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
甲型H1N1流感病毒是A型流感病毒，携带有H1N1亚型猪流感病毒毒株，包含有禽流感、猪流感和人流感三种流感病毒，预计今年全球将有约三千万人感染该病毒的危险．请用科学记数法表示：三千万（ ）
| A、3×106 |
| B、3×107 |
| C、3×108 |
| D、3×109 |
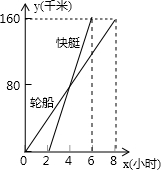如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象．根据图象下列结论错误的是（ ）| A、轮船的速度为20km/h |
| B、快艇的速度为40km/h |
| C、轮船比快艇先出发2h |
| D、快艇不能赶上轮船 |
如图，在△ABC中，DE∥FG∥BC，AD：DF：BF=1：2：3，BC=10cm．
如图，在平面直角坐标系中，四边形MNPO的顶点P的坐标是（3，4），且OM=OP，则顶点M的坐标是（ ）| A、（3，0） |
| B、（4，0） |
| C、（5，0） |
| D、（6，0） |