题目内容
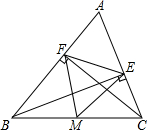 如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.(1)若EF=4,BC=10,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠MEF的度数.
考点:直角三角形斜边上的中线
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得EM=FM=
BC,然后根据三角形的周长的定义解答;
(2)根据等腰三角形的两底角相等求出∠BME,∠CME,再根据平角的定义求出∠EMF,然后根据等腰三角形两底角相等列式计算即可得解.
| 1 |
| 2 |
(2)根据等腰三角形的两底角相等求出∠BME,∠CME,再根据平角的定义求出∠EMF,然后根据等腰三角形两底角相等列式计算即可得解.
解答:解:(1)∵CF⊥AB,BE⊥AC,M为BC的中点,
∴EM=FM=
BC,
∵EF=4,BC=10,
∴△EFM的周长=EF+EM+FM=EF+BC=4+10=14;
(2)∵EM=BM=FM=CM=
BC,
∴∠ABC=∠BFM=50°,∠ACB=∠CEM=70°,
∴∠BME=180°-50°×2=80°,
∠CME=180°-70°×2=40°,
∴∠EMF=180°-80°-40°=60°,
∴∠MEF=
(180°-∠EMF)=
×(180°-60°)=60°.
∴EM=FM=
| 1 |
| 2 |
∵EF=4,BC=10,
∴△EFM的周长=EF+EM+FM=EF+BC=4+10=14;
(2)∵EM=BM=FM=CM=
| 1 |
| 2 |
∴∠ABC=∠BFM=50°,∠ACB=∠CEM=70°,
∴∠BME=180°-50°×2=80°,
∠CME=180°-70°×2=40°,
∴∠EMF=180°-80°-40°=60°,
∴∠MEF=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,熟记性质是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
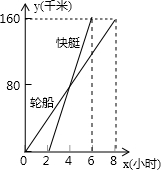 如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象.根据图象下列结论错误的是( )
如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象.根据图象下列结论错误的是( )| A、轮船的速度为20km/h |
| B、快艇的速度为40km/h |
| C、轮船比快艇先出发2h |
| D、快艇不能赶上轮船 |
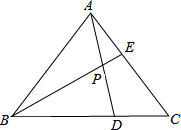 已知如图,在△ABC的边BC,AC上分别取点D、E,使BD=2CD,CE=2AE,AD与BE的交点为P,求证:S△EPA:S△APB:S△BPD:S△ABC=1:6:8:21.
已知如图,在△ABC的边BC,AC上分别取点D、E,使BD=2CD,CE=2AE,AD与BE的交点为P,求证:S△EPA:S△APB:S△BPD:S△ABC=1:6:8:21. 如图已知,在△ABC中,∠A=60°,BD是∠ABC的平分线.
如图已知,在△ABC中,∠A=60°,BD是∠ABC的平分线. 如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△ABC的面积为1,则阴影部分的面积为
如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△ABC的面积为1,则阴影部分的面积为