题目内容
7. 如图,点A,B的坐标分别为(1,2),(2,1),设点P(m,0),若△PAB的面积为4,则m的值为-1或7.
如图,点A,B的坐标分别为(1,2),(2,1),设点P(m,0),若△PAB的面积为4,则m的值为-1或7.
分析 延长AB交x轴于点C,如图,运用待定系数法可求出直线AB的解析式,从而可求出点C的坐标,再运用割补法可求出PC的值,结合点C的坐标就可求出m的值.
解答  解:延长AB交x轴于点C,如图,
解:延长AB交x轴于点C,如图,
设直线AB的解析式为y=ax+n,
则有$\left\{\begin{array}{l}{a+n=2}\\{2a+n=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{n=3}\end{array}\right.$,
∴直线AB的解析式为y=-x+3.
∵点C是直线y=-x+3与x轴的交点,
∴点C的坐标为(3,0),OC=3,
∵S△PAB=2,
∴S△PAB=S△PAC-S△PBC=$\frac{1}{2}$×PC×2-$\frac{1}{2}$×PC×1=$\frac{1}{2}$PC=2,
∴PC=4.
∵C(3,0),P(m,0),
∴|m-3|=4,
∴m=-1或7.
故答案为:-1或7.
点评 本题主要考查了运用待定系数法求直线、运用割补法求三角形的面积等知识,运用割补法是解决本题的关键,需要注意的是线段的长度确定,点的坐标未必确定.

练习册系列答案
相关题目
18.已知点P(1-2a,a+3)在第二象限,则a的取值范围是( )
| A. | a<-3 | B. | a>$\frac{1}{2}$ | C. | -$\frac{1}{2}$<a<3 | D. | -3<a<$\frac{1}{2}$ |
15.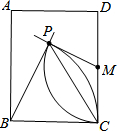 如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )
如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )
 如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )
如图,长方形ABCD中,M为CD中点,分别以点B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P.若∠PMC=110°,则∠BPC的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
19.二次函数y=x2-4x-4的顶点坐标为( )
| A. | (2,-8) | B. | (2,8) | C. | (-2,8) | D. | (-2,-8) |
16.今年,我省启动了“爱护眼睛保护视力”仪式,某小学为了了解各年级戴近视镜的情况,对一到六年级近视的学生进行了统计,得到每个年级的近视的儿童人数分别为20,30,20,34,36,40,对于这组数据,下列说法错误的是( )
| A. | 平均数是30 | B. | 众数是20 | C. | 中位数是34 | D. | 方差是$\frac{176}{3}$ |
12.如果x2+4xy+4y2=0,那么$\frac{x}{y}$的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |