题目内容
16.今年,我省启动了“爱护眼睛保护视力”仪式,某小学为了了解各年级戴近视镜的情况,对一到六年级近视的学生进行了统计,得到每个年级的近视的儿童人数分别为20,30,20,34,36,40,对于这组数据,下列说法错误的是( )| A. | 平均数是30 | B. | 众数是20 | C. | 中位数是34 | D. | 方差是$\frac{176}{3}$ |
分析 根据方差、众数、平均数和中位数的计算公式和定义分别进行解答即可.
解答 解:A、平均数是:(20+30+20+34+36+40)÷6=30,故本选项正确;
B、20出现了2次,出现的次数最多,则众数是20,故本选项正确;
C、把这组数据从小到大排列为20,20,30,34,36,40,
最中间的数是(30+34)÷2=32,则中位数是32,故本选项错误;
D、方差是:$\frac{1}{6}$[2(20-30)2+(30-30)2+(34-30)2+(36-30)2+(40-30)2]=$\frac{176}{3}$,故本选项正确.
则说法错误的是C;
故选C.
点评 此题考查了方差、众数、平均数和中位数的定义.用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | (a2b)3=a6b3 | B. | a6÷a2=a3(a≠0) | C. | a-2=-$\frac{1}{{a}^{2}}$(a≠0) | D. | $\root{3}{(-2)^{3}}$=2 |
11.下列命题是真命题的是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线相等的四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
1.△ABC的三边之比为3:4:5,与其相似的△DEF的最短边是9cm,则其最长边的长是( )
| A. | 5 cm | B. | 10 cm | C. | 15 cm | D. | 30 cm |
20.无论a取何值,下列代数式的值总是正数的有( )
|a+1|,a2+3,a+100,|a|+1,a2n+1(n是整数)
|a+1|,a2+3,a+100,|a|+1,a2n+1(n是整数)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.抛物线y=$\frac{1}{2}$x2-2x+$\frac{3}{2}$与x轴的交点坐标是( )
| A. | (1,0) | B. | (3,0) | C. | (1,0)或(3,0) | D. | (1,0)或(-3,0) |
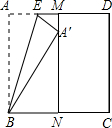 如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N=$\frac{\sqrt{2n-1}}{n}$.
如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N=$\frac{\sqrt{2n-1}}{n}$. 如图,点A,B的坐标分别为(1,2),(2,1),设点P(m,0),若△PAB的面积为4,则m的值为-1或7.
如图,点A,B的坐标分别为(1,2),(2,1),设点P(m,0),若△PAB的面积为4,则m的值为-1或7.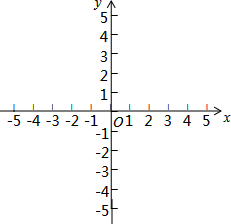 对于自变量x的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.分段函数在不同的定义域上,函数的表达式也不同.例如:y=$\left\{\begin{array}{l}{{x}^{2}-2x(x≥0)}\\{2x(x<0)}\end{array}\right.$是分段函数.当x≥0时,它是二次函数y=x2-2x,当x<0时,它是正比例函数y=2x.
对于自变量x的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.分段函数在不同的定义域上,函数的表达式也不同.例如:y=$\left\{\begin{array}{l}{{x}^{2}-2x(x≥0)}\\{2x(x<0)}\end{array}\right.$是分段函数.当x≥0时,它是二次函数y=x2-2x,当x<0时,它是正比例函数y=2x.