题目内容
18.已知点P(1-2a,a+3)在第二象限,则a的取值范围是( )| A. | a<-3 | B. | a>$\frac{1}{2}$ | C. | -$\frac{1}{2}$<a<3 | D. | -3<a<$\frac{1}{2}$ |
分析 根据第二象限内点的横坐标小于零,纵坐标大于零,可得不等式组,根据解不等式组,可得答案.
解答 解:由点P(1-2a,a+3)在第二象限,得$\left\{\begin{array}{l}{1-2a<0}\\{a+3>0}\end{array}\right.$.
解得a>$\frac{1}{2}$,
故选B.
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9. 如图,将一张边长为m的正方形纸片,第一次剪成四个大小形状一样的小正方形,然后再将其中的一个小正方形按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下表.
如图,将一张边长为m的正方形纸片,第一次剪成四个大小形状一样的小正方形,然后再将其中的一个小正方形按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下表.
(1)观察图形,填写下表:
(2)推测当剪第n次时,正方形的个数为3n+1;最小正方形边长为$\frac{m}{{2}^{n}}$.(都用含m或n的代数式表示)
 如图,将一张边长为m的正方形纸片,第一次剪成四个大小形状一样的小正方形,然后再将其中的一个小正方形按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下表.
如图,将一张边长为m的正方形纸片,第一次剪成四个大小形状一样的小正方形,然后再将其中的一个小正方形按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下表.(1)观察图形,填写下表:
| 剪的次数 | 1 | 2 | 3 |
| 正方形个数 | 4 | 7 | 10 |
| 最小正方形边长 | $\frac{1}{2}$m | $\frac{1}{4}$m | $\frac{1}{8}$m |
10.不等式2x+3>3x+2的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
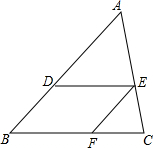 如图,△ABC中,DE∥BC,EF∥AB,若AB=8,BD=3,BF=4,则CF=$\frac{12}{5}$.
如图,△ABC中,DE∥BC,EF∥AB,若AB=8,BD=3,BF=4,则CF=$\frac{12}{5}$.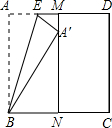 如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N=$\frac{\sqrt{2n-1}}{n}$.
如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N=$\frac{\sqrt{2n-1}}{n}$. 已知有理数a、b、c在数轴上的对应点如图所示,化简:|a-b|-|a+b|+|a|+|a-c|.
已知有理数a、b、c在数轴上的对应点如图所示,化简:|a-b|-|a+b|+|a|+|a-c|.
 如图,点A,B的坐标分别为(1,2),(2,1),设点P(m,0),若△PAB的面积为4,则m的值为-1或7.
如图,点A,B的坐标分别为(1,2),(2,1),设点P(m,0),若△PAB的面积为4,则m的值为-1或7.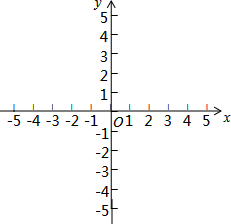 对于自变量x的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.分段函数在不同的定义域上,函数的表达式也不同.例如:y=$\left\{\begin{array}{l}{{x}^{2}-2x(x≥0)}\\{2x(x<0)}\end{array}\right.$是分段函数.当x≥0时,它是二次函数y=x2-2x,当x<0时,它是正比例函数y=2x.
对于自变量x的不同的取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.分段函数在不同的定义域上,函数的表达式也不同.例如:y=$\left\{\begin{array}{l}{{x}^{2}-2x(x≥0)}\\{2x(x<0)}\end{array}\right.$是分段函数.当x≥0时,它是二次函数y=x2-2x,当x<0时,它是正比例函数y=2x.