题目内容
18.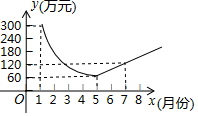 为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )
为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )| A. | 5月份该厂的月利润最低 | |
| B. | 治污改造完成后,每月利润比前一个月增加30万元 | |
| C. | 治污改造前后,共有6个月的月利润不超过120万元 | |
| D. | 治污改造完成后的第8个月,该厂月利润达到300万月 |
分析 直接利用已知点求出一次函数与反比例函数的解析式进而分别分析得出答案.
解答 解:A、由函数图象可得,5月份该厂的月利润最低为60万,故此选选项正确,不合题意;
B、治污改造完成后,从5月到7月,利润从60万到120万,故每月利润比前一个月增加30万元,故此选选项正确,不合题意;
C、设反比例函数解析式为:y=$\frac{a}{x}$,
则a=300,
故y=$\frac{300}{x}$,
则120=$\frac{300}{x}$,
解得:x=$\frac{5}{2}$,
则只有3月,4月,5月,6月,7月共5个月的利润不超过120万元,故此选项错误,符合题意.
D、设一次函数解析式为:y=kx+b,
则$\left\{\begin{array}{l}{5k+b=60}\\{7k+b=120}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=30}\\{b=-90}\end{array}\right.$,
故一次函数解析式为:y=30x-90,
故y=300时,300=30x-90,
解得:x=13,
则治污改造完成后的第8个月,该厂月利润达到300万,故此选项正确,不合题意.
故选:C.
点评 此题主要考查了一次函数与反比函数的应用,正确得出函数解析是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列图形都是由同样大小的黑色三角形按一定规律所组成的,其中第①个图形中一共有 4 个黑色三角形,第②个图形中一共有 8 个黑色三角形,第③个图形中一共有13 个黑色三角形,…,按此规律排列下去,第⑦个图形中黑色三角形的个数是( )


| A. | 65 | B. | 53 | C. | 43 | D. | 34 |
9.下列运算中正确的是( )
| A. | 3a-a=3 | B. | a2•a3=a6 | C. | (-2a)3=-6a 3 | D. | ab2÷a=b 2 |
6.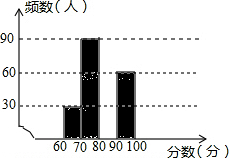 2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.
2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.
请你根据表中提供的信息,解答下列问题:
(1)此次调查的样本容量为300;
(2)在表中:m=120,n=0.30;
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,那么请你估计该校学生笔试成绩的优秀人数大约是1200名.
 2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.
2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
(1)此次调查的样本容量为300;
(2)在表中:m=120,n=0.30;
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,那么请你估计该校学生笔试成绩的优秀人数大约是1200名.
13.下列函数中,y随x增大而减少的是( )
| A. | y=2x-1 | B. | y=-x+3 | C. | y=$\frac{1}{2}$x+2 | D. | y=2x |
7.要使分式$\frac{3}{x-2}$有意义,则x的取值范围是( )
| A. | x≠-2 | B. | x>2 | C. | x<2 | D. | x≠2 |