题目内容
6.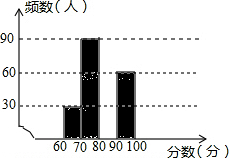 2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.
2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
(1)此次调查的样本容量为300;
(2)在表中:m=120,n=0.30;
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,那么请你估计该校学生笔试成绩的优秀人数大约是1200名.
分析 (1)根据百分比=$\frac{所占人数}{总人数}$计算即可.
(2)根据m的值画出条形图即可;
(3)用样本估计总体的思想解决问题即可;
解答 解:(1)此次调查的样本容量为30÷0.1=300人,
故答案为300.
(2)m=300×0.4=120人,n=$\frac{90}{300}$=0.30.
故答案为120,0.30.
(3)条形图如图所示,
(4)2000×(0.4+0.2)=1200人,
估计该校学生笔试成绩的优秀人数大约是1200人,
故答案为1200.
点评 本题考查频数分布直方图、频数分布表、样本估计总体的思想等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列运算正确的是( )
| A. | 2x2•6x4=12x8 | B. | 4a2-a2=3 | C. | (x+y)2=x2+y2 | D. | (y4)m÷(y3)m=ym |
11.将(-30)0,(-3)2,($\frac{1}{5}$)-1这三个数按从小到大的顺序排列,正确的结果是( )
| A. | ($\frac{1}{5}$)-1<(-30)0<(-3)2 | B. | (-30)0<(-3)2<($\frac{1}{5}$)-1 | C. | (-3)2<($\frac{1}{5}$)-1<(-30)0 | D. | (-30)0<($\frac{1}{5}$)-1<(-3)2 |
18.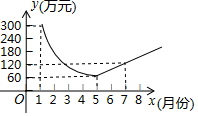 为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )
为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )
 为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )
为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )| A. | 5月份该厂的月利润最低 | |
| B. | 治污改造完成后,每月利润比前一个月增加30万元 | |
| C. | 治污改造前后,共有6个月的月利润不超过120万元 | |
| D. | 治污改造完成后的第8个月,该厂月利润达到300万月 |
15.某校为了备战2018体育中考,因此在八年级抽取了50名女学生进行“一分钟仰卧起坐”测试,测试的情况绘制成表格如下:
(1)通过计算算得出这50名女学生进行“一分钟仰卧起坐”的平均数是30,请写出这50名女学生进行“一分钟仰卧起坐”的众数和中位数,它们分别是28、28.
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
| 个数 | 16 | 22 | 25 | 28 | 29 | 30 | 35 | 37 | 40 | 42 | 45 | 46 |
| 人数 | 2 | 1 | 7 | 18 | 1 | 9 | 5 | 2 | 1 | 1 | 1 | 2 |
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
16.下列函数中,自变量x的取值范围是x>3的是( )
| A. | y=x-3 | B. | $y=\frac{1}{x-3}$ | C. | $y=\sqrt{x-3}$ | D. | y=$\frac{1}{\sqrt{x-3}}$ |
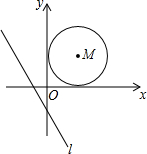 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(2,2)为圆心,2个单位长度为半径的⊙M以每秒1个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为$\frac{13±2\sqrt{13}}{3}$秒.
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(2,2)为圆心,2个单位长度为半径的⊙M以每秒1个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为$\frac{13±2\sqrt{13}}{3}$秒.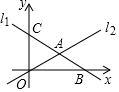 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+8分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{3}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+8分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{3}$x交于点A.