题目内容
3.已知反比例函数y=$\frac{1-k}{x}$的图象经过点A(2,-4).(1)求k的值;
(2)它的图象在第二、四象限内,在各象限内,y随x增大而增大;(填变化情况)
(3)当-2≤x≤-$\frac{1}{2}$时,求y的取值范围.
分析 (1)把点A的坐标代入函数解析式,利用待定系数法确定函数关系式;
(2)根据(1-k)的符号来确定函数图象的性质;
(3)由函数图象的性质解答.
解答 解:(1)依题意得:1-k=2×(-4)=-8,所以k=9;
(2)∵1-k=-8<0,
∴反比例函数y=$\frac{1-k}{x}$的图象经过第二、四象限,且在各象限内,y随x增大而增大;
故答案是:二、四,增大;
(3)由(1)得反比例函数表达式为$y=-\frac{8}{x}$,
当x=-2时,y=4,
当$x=-\frac{1}{2}$时,y=16,
所以,当$-2≤x≤-\frac{1}{2}$时,4≤y≤16.
点评 本题考查了反比例函数的性质和反比例函数图象上点的坐标特征,通过计算得到k的值是解题的关键所在.

练习册系列答案
相关题目
13.下列说法错误的是( )
| A. | 若a=b,则a+c=b+c | B. | 若a=b,则a-c=b-c | C. | 若a=b,则ac=bc | D. | 若a=b,则$\frac{a}{c}$=$\frac{b}{c}$ |
11.将(-30)0,(-3)2,($\frac{1}{5}$)-1这三个数按从小到大的顺序排列,正确的结果是( )
| A. | ($\frac{1}{5}$)-1<(-30)0<(-3)2 | B. | (-30)0<(-3)2<($\frac{1}{5}$)-1 | C. | (-3)2<($\frac{1}{5}$)-1<(-30)0 | D. | (-30)0<($\frac{1}{5}$)-1<(-3)2 |
18.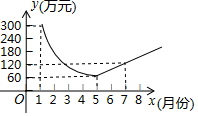 为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )
为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )
 为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )
为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )| A. | 5月份该厂的月利润最低 | |
| B. | 治污改造完成后,每月利润比前一个月增加30万元 | |
| C. | 治污改造前后,共有6个月的月利润不超过120万元 | |
| D. | 治污改造完成后的第8个月,该厂月利润达到300万月 |
15.某校为了备战2018体育中考,因此在八年级抽取了50名女学生进行“一分钟仰卧起坐”测试,测试的情况绘制成表格如下:
(1)通过计算算得出这50名女学生进行“一分钟仰卧起坐”的平均数是30,请写出这50名女学生进行“一分钟仰卧起坐”的众数和中位数,它们分别是28、28.
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
| 个数 | 16 | 22 | 25 | 28 | 29 | 30 | 35 | 37 | 40 | 42 | 45 | 46 |
| 人数 | 2 | 1 | 7 | 18 | 1 | 9 | 5 | 2 | 1 | 1 | 1 | 2 |
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
13. 为了了解学生在一年中的课外阅读量,语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A:10本以下;B:10~15本;C:16~20本;D:20本以上.根据调查结果制作了下列的两幅统计图表:
为了了解学生在一年中的课外阅读量,语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A:10本以下;B:10~15本;C:16~20本;D:20本以上.根据调查结果制作了下列的两幅统计图表:
根据以上信息回答下列问题:
(1)在这次调查中一共抽查了200名学生;
(2)表中x,y的值分别为:x=60,y=80;
(3)在扇形统计图中,计算C部分所对应的扇形的圆心角度数;
(4)根据抽样调查结果,请估计九年级学生一年阅读课外书20本以上的学生人数.
 为了了解学生在一年中的课外阅读量,语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A:10本以下;B:10~15本;C:16~20本;D:20本以上.根据调查结果制作了下列的两幅统计图表:
为了了解学生在一年中的课外阅读量,语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A:10本以下;B:10~15本;C:16~20本;D:20本以上.根据调查结果制作了下列的两幅统计图表:| 各种情况人数统计频数分布表 | ||||
| 课外阅读情况 | A | B | C | D |
| 频数 | 20 | x | y | 40 |
(1)在这次调查中一共抽查了200名学生;
(2)表中x,y的值分别为:x=60,y=80;
(3)在扇形统计图中,计算C部分所对应的扇形的圆心角度数;
(4)根据抽样调查结果,请估计九年级学生一年阅读课外书20本以上的学生人数.