题目内容
8．若$\sqrt{a-3}$+（b+2）2=0，则点M（a，b）关于x轴的对称点的坐标为（ 3，2 ）．分析 利用非负数的性质求得a、b的值，即可求得点M的坐标，根据关于x轴对称的点，横坐标相同，纵坐标互为相反数，进而得出答案．
解答 解：由$\sqrt{a-3}$+（b+2）2=0，得
a-3=0，b+2=0，
所以a=3，b=-2，
∴M（3，-2），
∴点M（a，b）关于x轴的对称点的坐标为：（ 3，2 ）；
故答案是：（ 3，2 ）．
点评 此题主要考查了关于x轴对称点的性质，解决本题的关键是掌握好对称点的坐标规律：
（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；
（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；
（3）关于原点对称的点，横坐标与纵坐标都互为相反数．
练习册系列答案
相关题目
18．
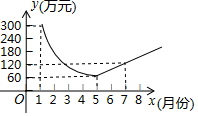为了建设生态丽水，某工厂在一段时间内限产并投入资金进行治污改造，下列描述的是月利润y（万元）关于月份x之间的变化关系，治污改造完成前是反比例函数图象的一部分，治污改造完成后是一次函数图象的一部分，则下列说法不正确的是（ ）
为了建设生态丽水，某工厂在一段时间内限产并投入资金进行治污改造，下列描述的是月利润y（万元）关于月份x之间的变化关系，治污改造完成前是反比例函数图象的一部分，治污改造完成后是一次函数图象的一部分，则下列说法不正确的是（ ）| A． | 5月份该厂的月利润最低 | |
| B． | 治污改造完成后，每月利润比前一个月增加30万元 | |
| C． | 治污改造前后，共有6个月的月利润不超过120万元 | |
| D． | 治污改造完成后的第8个月，该厂月利润达到300万月 |
19．下列四组线段中，可以构成直角三角形的是（ ）
| A． | 2，3，4 | B． | 4，5，6 | C． | 1.5，2.5，3 | D． | 1，$\sqrt{2}$，$\sqrt{3}$ |
16．下列函数中，自变量x的取值范围是x＞3的是（ ）
| A． | y=x-3 | B． | $y=\frac{1}{x-3}$ | C． | $y=\sqrt{x-3}$ | D． | y=$\frac{1}{\sqrt{x-3}}$ |
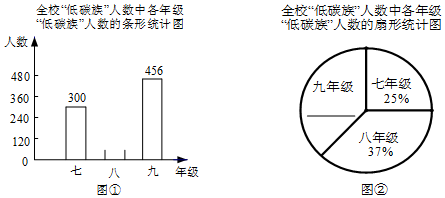
13．
为了了解学生在一年中的课外阅读量，语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查，调查的结果分为四种情况：A：10本以下；B：10～15本；C：16～20本；D：20本以上．根据调查结果制作了下列的两幅统计图表：
根据以上信息回答下列问题：
（1）在这次调查中一共抽查了200名学生；
（2）表中x，y的值分别为：x=60，y=80；
（3）在扇形统计图中，计算C部分所对应的扇形的圆心角度数；
（4）根据抽样调查结果，请估计九年级学生一年阅读课外书20本以上的学生人数．
为了了解学生在一年中的课外阅读量，语文老师在七年级1500名学生中采用随机抽样的方式进行了问卷调查，调查的结果分为四种情况：A：10本以下；B：10～15本；C：16～20本；D：20本以上．根据调查结果制作了下列的两幅统计图表：| 各种情况人数统计频数分布表 | ||||
| 课外阅读情况 | A | B | C | D |
| 频数 | 20 | x | y | 40 |
（1）在这次调查中一共抽查了200名学生；
（2）表中x，y的值分别为：x=60，y=80；
（3）在扇形统计图中，计算C部分所对应的扇形的圆心角度数；
（4）根据抽样调查结果，请估计九年级学生一年阅读课外书20本以上的学生人数．
20．科学家在实验中检测出某微生物约长0.000000036m，将0.000000036用科学记数法表示为（ ）
| A． | 3.6×10-8 | B． | 3.6×108 | C． | 3.6×10-7 | D． | 0.36×10-9 |
我县开展“美丽新野，创卫同行”活动，某校倡议学生利用双休日参加义务劳动，为了解同学们劳动情况，学校随机调查了100名同学的劳动时间，并用得到的数据绘制了一幅不完整的统计图，根据图中信息解答下列问题：
如图，在平行四边形ABCD中，AB=7，BC=10，∠C的平分线交AD于E，交BA的延长线于F，则AE+AF的值等于（ ）