题目内容
20.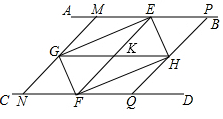 如图,AB∥CD,点E,F分别是AB,CD上,连结EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.
如图,AB∥CD,点E,F分别是AB,CD上,连结EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.(1)如果过点G作MN∥EF,分别交AB,CD于点M,N,过点H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形ANQP,求证:MNQP是菱形.
(2)在(1)的条件下,联结GH交EF于点K,则MEKG是什么四边形?并证明.
分析 (1)首先证明四边形EGFH是矩形,再证明四边形MGKE是菱形,利用可证四边形EKHP,四边形KFQH,四边形KFNG都是菱形,即可推出MN=NQ=PQ=PM,推出四边形MNQP是菱形;
(2)四边形MEKG是菱形.只要证明KE=KG,四边形MEKG是平行四边形即可;
解答 (1)证明:∵GE平分∠AEF,HE平分∠BEF,
∴∠GEH=90°,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵∠GEF=$\frac{1}{2}$∠AEF,∠GFE=$\frac{1}{2}$∠CFE,
∴∠GEF+∠GFE=90°,
同理∠EHF=90°,
∴四边形EGFH是矩形
∴EG=FH,KG=KE,
∴∠KEG=∠KGE=∠AEG,
∴ME∥GK,∵MG∥EK,
∴四边形MGKE是平行四边形,
∵KE=KG,
∴四边形MGKE是菱形,
同理可证四边形EKHP,四边形KFQH,四边形KFNG都是菱形,
∴MG=GN=NF=FQ=QH=HP=PE=EM,
∴MN=NQ=PQ=PM,
∴四边形MNQP是菱形.
(2)四边形MEKG是菱形.
理由:∵四边形EGFH是矩形
∴EG=FH,KG=KE,
∴∠KEG=∠KGE=∠AEG,
∴ME∥GK,∵MG∥EK,
∴四边形MGKE是平行四边形,
∵KE=KG,
∴四边形MGKE是菱形.
点评 本题考查菱形的判定和性质、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.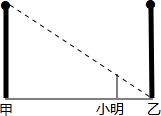 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )| A. | 7米 | B. | 8米 | C. | 9米 | D. | 10米 |
8.要使(x2+ax+1)(-6x3)的展开式中不含x4项,则a应等于( )
| A. | 6 | B. | -1 | C. | $\frac{1}{6}$ | D. | 0 |
15.若x2-y2=8,x+y=-4,则x-y的值是( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
5.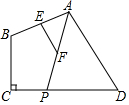 如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
 如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )
如图,已知四边形ABCD中,∠C=90°,点P是CD边上的动点,连接AP,E,F分别是AB,AP的中点,当点P在CD上从点D向点C移动过程中,下列结论成立的是( )| A. | 线段EF的长先减小后增大 | B. | 线段EF的长不变 | ||
| C. | 线段EF的长逐渐增大 | D. | 线段EF的长逐渐减小 |
12. 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )| A. | 10 | B. | 17 | C. | 20 | D. | 21.5 |
14.若y=kx+b中,当x=-1时,y=1;当x=2时,y=-2,则k与b为( )
| A. | $\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{k=-1}\\{b=0}\end{array}}\right.$ | C. | $\left\{\begin{array}{l}k=1\\ b=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=1\\ b=-4\end{array}\right.$ |
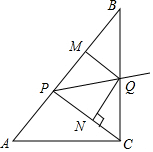 如图,已知:在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.
如图,已知:在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.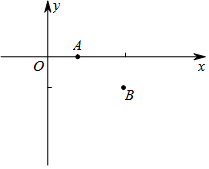 如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).
如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).