题目内容
13.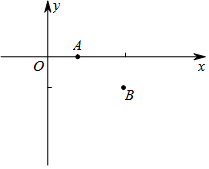 如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).
如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).
分析 首先求出直线AB的解析式为y=-$\frac{1}{2}$x+$\frac{1}{2}$再求出过点A垂直AB的直线为y=2x-2,过点B垂直AB的直线为y=2x-7,分三种情形讨论即可解决问题.
解答 解:如图,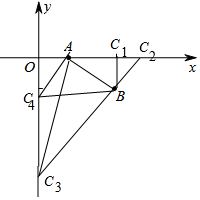
∵A(-1,0),B(3,-1),
∴直线AB的解析式为y=-$\frac{1}{2}$x+$\frac{1}{2}$,
过点A垂直AB的直线为y=2x-2,过点B垂直AB的直线为y=2x-7,
∴当C1为直角顶点时,C1(3,0),
当B为直角顶点时,C2($\frac{7}{2}$,0),C3(0,-7)
当A为直角顶点时,C4(0,-2),
综上所述,满足条件的点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).
故答案为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).
点评 本题考查勾股定理、坐标与图形的性质、直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,注意不能漏解.

练习册系列答案
相关题目
19.下列计算中,正确的是( )
| A. | a•a=2a | B. | x+x4=x5 | C. | x3•x2=x5 | D. | 2a2•a-1=2a3 |
18.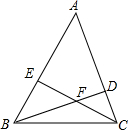 如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
 如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )| A. | 20$\sqrt{3}$ | B. | 25$\sqrt{3}$ | C. | 30$\sqrt{3}$ | D. | 40$\sqrt{3}$ |
2.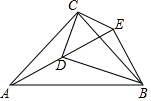 如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
 如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
3.为了解某市参加中考的40073名学生的身高情况,抽查了其中1000名学生的身高进行统计分析.下面叙述正确的是( )
| A. | 40073名学生是总体 | |
| B. | 每名学生是总体的一个个体 | |
| C. | 本次调查是全面调查 | |
| D. | 1000名学生的身高是总体的一个样本 |
 如图,AB∥CD,点E,F分别是AB,CD上,连结EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.
如图,AB∥CD,点E,F分别是AB,CD上,连结EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H. 如图,在△ABC中,∠BAC=90°,AB=AC,点O是BC中点,点D、E分别在BA、AC的延长线上,且OD⊥OE,说明OD=OE.
如图,在△ABC中,∠BAC=90°,AB=AC,点O是BC中点,点D、E分别在BA、AC的延长线上,且OD⊥OE,说明OD=OE. 工人师傅盖房子时,常将房梁设计如图所示的图形,使其牢固不变形,这是利用三角形稳定性.
工人师傅盖房子时,常将房梁设计如图所示的图形,使其牢固不变形,这是利用三角形稳定性.