题目内容

8．要使（x2+ax+1）（-6x3）的展开式中不含x4项，则a应等于（　　）
A．6B．-1C．$\frac{1}{6}$D．0

分析 直接利用单项式乘以多项式运算法则结合已知得出a的值．

解答 解：∵（x2+ax+1）（-6x3）的展开式中不含x4项，
∴（x2+ax+1）（-6x3）=-6x5-6ax4-6x3，中-6a=0，
解得：a=0．
故选：D．

点评 此题主要考查了单项式乘以多项式，正确掌握运算法则是解题关键．

练习册系列答案
相关题目
18．如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C、D不重合）．

（1）如图①，当α=90°时，求证：DE+DF=AD．
（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为$DE+DF=\frac{1}{2}AD$，请给出证明．
（3）在（2）的条件下，将∠QPN绕点P旋转，若旋转过程中∠QPN的边PQ与边AD的延长线交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．
19．下列计算中，正确的是（　　）
A．a•a=2aB．x+x4=x5C．x3•x2=x5D．2a2•a-1=2a3
16．对于一个三位正整数t，将各数位上的数字重新排序后（包括本身），得到一个新的三位数$\overline{abc}$（a≤c），在所有重新排列的三位数中，当|a+c-2b|最小时，称此时的$\overline{abc}$为t的“最优组合”，并规定F（t）=|a-b|-|b-c|，例如：124重新排序后为：142、214、因为|1+4-4|=1，|1+2-8|=5，|2+4-2|=4，所以124为124的“最优组合”，此时F（124）=-1．
（1）三位正整数t中，有一个数位上的数字是另外两数位上的数字的平均数，求证：F（t）=0
（2）一个正整数，由N个数字组成，若从左向右它的第一位数能被1整除，它的前两位数能被2整除，前三位数能被3整除，…，一直到前N位数能被N整除，我们称这样的数为“善雅数”．例如：123的第一位数1能披1整除，它的前两位数12能被2整除，前三位数123能被3整除，则123是一个“善雅数”．若三位“善雅数”m=200+10x+y（0≤x≤9，0≤y≤9，x、y为整数），m的各位数字之和为一个完全平方数，求出所有符合条件的“善雅数”中F（m）的最大值．
3．如图，AB是⊙O的直径，弦CD⊥AB于H，若BH=2，CD=8，则⊙O的半径长为（　　）
A．2B．3C．4D．5
13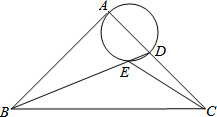．如图，在等腰直角△ABC中，∠BAC=90°，AB=AC，BC=4$\sqrt{2}$，点D是AC上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值是（　　）
A．2B．4C．$2\sqrt{2}-2$D．$2\sqrt{5}-2$
20．如图，AB∥CD，点E，F分别是AB，CD上，连结EF，∠AEF，∠CFE的平分线交于点G，∠BEF，∠DFE的平分线交于点H．
（1）如果过点G作MN∥EF，分别交AB，CD于点M，N，过点H作PQ∥EF，分别交AB，CD于点P，Q，得到四边形ANQP，求证：MNQP是菱形．
（2）在（1）的条件下，联结GH交EF于点K，则MEKG是什么四边形？并证明．
1．如图，在△ABC中，∠BAC=90°，AB=AC，点O是BC中点，点D、E分别在BA、AC的延长线上，且OD⊥OE，说明OD=OE．
2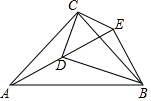．如图，已知△ABC是等腰直角三角形，其内部有一点D，连接BD，以BD为斜边作等腰直角三角形BDE，连接AD、CD、CE，若CD=1，AD=2，∠DCE=90°，则DE的长是 （　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网