题目内容
13．
如图，在△ABC中，AD是△ABC的高线，AE是△ABC的角平分线．已知∠B=40°，∠C=70°．求∠DAE的度数．
分析 根据三角形的内角和定理求出∠BAC的度数，再根据AD是△BAC的角平分线，求出∠DAC的度数，减去∠EAC的度数即为∠DAE的度数．
解答 解：∵∠B=40°，∠C=70°，
∴∠BAC=∠180°-40°-70°=70°，
∵AD是△BAC的角平分线，
∴∠DAC=70°×$\frac{1}{2}$=35°，
∵∠AED=90°，∠C=70°，
∴∠EAC=90°-70°=20°，
∴∠DAE=35°-20°=15°．
点评 本题考查三角形的内角和定理及角平分线的性质，高线的性质，解答的关键是三角形的内角和定理，一定要熟稔于心．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
3．已知正三角形的边长为2，则它的内切圆和外接圆组成的圆环面积为（ ）
| A． | 3π | B． | 2π | C． | π | D． | $\frac{1}{2}$π |
已知直线y=-x+4．
18．甲、乙两人骑自行车比赛，若甲先骑30分钟，则乙出发后50分钟可追上甲，设甲、乙每小时分别骑x千米、y千米，则可列方程（ ）
| A． | 30x=50y | B． | $\frac{1}{2}x=（{\frac{1}{2}+\frac{5}{6}}）y$ | C． | （30+50）x=50y | D． | $（{\frac{1}{2}+\frac{5}{6}}）x=\frac{5}{6}y$ |
如图，已知CD∥BF，∠B+∠D=180°，求证：AB∥DE．
4．
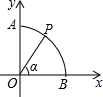如图，以坐标原点O为圆心，半径为1的弧交坐标轴于A，B两点，P是$\widehat{AB}$上一点（不与A，B重合），连接OP，设∠POB=α，则点P的坐标是（ ）
如图，以坐标原点O为圆心，半径为1的弧交坐标轴于A，B两点，P是$\widehat{AB}$上一点（不与A，B重合），连接OP，设∠POB=α，则点P的坐标是（ ）| A． | （sinα，sinα） | B． | （cosα，cosα） | C． | （sinα，cosα） | D． | （cosα，sinα） |