题目内容
4.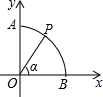 如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (sinα,cosα) | D. | (cosα,sinα) |
分析 作PC⊥OB于C,根据正弦、余弦的定义分别求出OC、PC,得到点P的坐标.
解答 解: 作PC⊥OB于C,
作PC⊥OB于C,
在Rt△POC中,OC=OP×cosα=cosα,
PC=OP×sinα=sinα,
∴点P的坐标为(cosα,sinα),
故选:D.
点评 本题考查的是解直角三角形、坐标与图形性质,掌握正弦、余弦的定义是解题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
10. 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠B=( )
如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠B=( )
 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠B=( )
如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠B=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
16.下列各组数中互为相反数的是( )
| A. | $\frac{1}{2}$与-0.2 | B. | -$\frac{1}{3}$与0.333 | C. | -2.25与2$\frac{1}{4}$ | D. | 5与-(-5) |
 如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.已知∠B=40°,∠C=70°.求∠DAE的度数.
如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.已知∠B=40°,∠C=70°.求∠DAE的度数.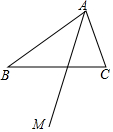 已知,如图,△ABC,射线AM平分∠BAC
已知,如图,△ABC,射线AM平分∠BAC 如图,∠ACB为钝角,用尺规作出△ABC的边AC上的高(不写作法,但要保留作图痕迹)
如图,∠ACB为钝角,用尺规作出△ABC的边AC上的高(不写作法,但要保留作图痕迹)