题目内容
4. 已知直线y=-x+4.
已知直线y=-x+4.(1)直接写出直线与x轴、y轴的交点A、B的坐标;
(2)画出图象;
(3)求直线与坐标轴围成的三角形的面积.
分析 (1)根据题意,分析可得在y=-x+4中,当x=4时,y=0,x=0时,y=4,据此可得点A、B的坐标;
(2)过点A、B画直线即可作出图象;
(3)根据三角形的面积公式计算即可.
解答 解:(1)令y=0得x=4,令x=0得y=4,
可得A点坐标为(4,0),
B点坐标为(0,4);
(2)如图所示: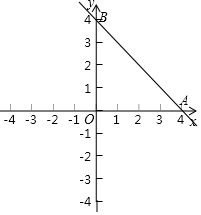
(3)∵A(4,0),B(0,4),
∴OA=4,OB=4,
∴S△AOB=$\frac{1}{2}$•OA•OB=$\frac{1}{2}$×4×4=8,
∴直线与坐标轴围成的三角形的面积为8.
点评 本题考查了一次函数的图象的图象:经过两点(0,b)、(-$\frac{b}{k}$,0)或(1,k+b)作直线y=kx+b.一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).也考查了一次函数图象上点的坐标特征以及三角形的面积.

练习册系列答案
相关题目
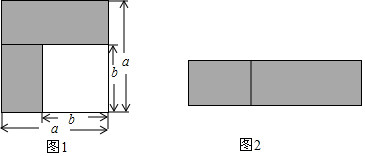
19.如图1所示,四边形ABCD为正方形,对角线AC,BD相交于点O,动点P在正方形的边和对角线上匀速运动.如果点P运动的时间为x,点P与点A的距离为y,且表示y与x的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )


| A. | A→B→C→A | B. | A→B→C→D | C. | A→D→O→A | D. | A→O→B→C |
9.下列电视台标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (ab)2=a2b2 | C. | (a2)3=a5 | D. | a6÷a2=a3 |
16.下列各组数中互为相反数的是( )
| A. | $\frac{1}{2}$与-0.2 | B. | -$\frac{1}{3}$与0.333 | C. | -2.25与2$\frac{1}{4}$ | D. | 5与-(-5) |
 如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.已知∠B=40°,∠C=70°.求∠DAE的度数.
如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.已知∠B=40°,∠C=70°.求∠DAE的度数.