题目内容
8.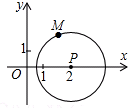 如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.
如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.
分析 当$\frac{b}{a}$有最大值时,得出tan∠MOP有最大值,推出当OM与圆相切时,tan∠MOP有最大值,根据解直角三角形得出tan∠MOP=$\frac{MP}{OM}$,由勾股定理求出OM,代入即可得出最大值,进而得出最小值,即可得出答案.
解答  解:如图所示:
解:如图所示:
当$\frac{b}{a}$有最大值时,即tan∠MOP有最大值,
也就是当OM与圆相切时,tan∠MOP有最大值,
此时tan∠MOP=$\frac{MP}{OM}$,
在Rt△OMP中,由勾股定理得:OM=$\sqrt{O{P}^{2}-P{M}^{2}}$=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
则tan∠MOP=$\frac{b}{a}$=$\frac{MP}{OM}$=$\sqrt{3}$,
同理可得:当OM在第四象限,则tan∠MOP=$\frac{b}{a}$=-$\sqrt{3}$,
故t的取值范围是:-$\sqrt{3}$≤t≤$\sqrt{3}$.
故答案为:-$\sqrt{3}$≤t≤$\sqrt{3}$.
点评 本题考查了解直角三角形、勾股定理、坐标与图形性质、切线的性质等知识点,关键是找出符合条件的M的位置,题目比较典型,但是有一定的难度.

练习册系列答案
相关题目
3.在火车站,通常可看到列车运行时刻表,T13列车由北京开往上海,T14列车由上海开往北京,这两次列车每天各发一列车,自北京到上海铁路线长1462km,请根据下表提供的信息进行分析:
北京与上海之间往返的T13、T14列车运行时刻表如下:
根据列车运行时刻表估算,T13与T14列车相遇地点距北京大约多远(铁路线长保留整数)?
北京与上海之间往返的T13、T14列车运行时刻表如下:
| 北京 | 天津西 | 济南 | 上海 | ||
| T13 | 到站时间 | … | 16:11 | 20:11 | 8:04 |
| 发车时间 | 14:40 | 16:16 | 20:23 | … | |
| T14 | 到站时间 | 9:03 | 7:23 | 3:14 | … |
| 发车时间 | … | 7:28 | 3:26 | 15:45 |
20.如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)=1,d(102)=2.
那么:d(103)=3,d(10-2)=-2
(2)劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d( $\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:
$\frac{d({a}^{3})}{d(a)}$=2d(a)(a为正数).
若d(3)=0.4771,则d(9)=0.9542,d($\frac{3}{10}$)=-0.5229;
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
(1)根据劳格数的定义,填空:d(10)=1,d(102)=2.
那么:d(103)=3,d(10-2)=-2
(2)劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d( $\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:
$\frac{d({a}^{3})}{d(a)}$=2d(a)(a为正数).
若d(3)=0.4771,则d(9)=0.9542,d($\frac{3}{10}$)=-0.5229;
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
| x | 0.8 | 2 | 3.2 | 4 | 5 | 8 |
| d(x) | 6a-3b+1 | 2a-b | 10a-5b | 4a-2b | 1-2a+b | 6a-3b |
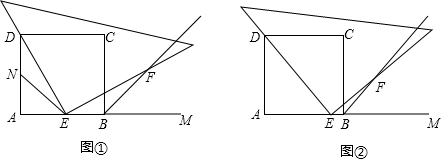
 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q. 如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是①③④(填代号).
如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是①③④(填代号).