题目内容
20.如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的b、n两个量之间的同一关系.(1)根据劳格数的定义,填空:d(10)=1,d(102)=2.
那么:d(103)=3,d(10-2)=-2
(2)劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d( $\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:
$\frac{d({a}^{3})}{d(a)}$=2d(a)(a为正数).
若d(3)=0.4771,则d(9)=0.9542,d($\frac{3}{10}$)=-0.5229;
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
| x | 0.8 | 2 | 3.2 | 4 | 5 | 8 |
| d(x) | 6a-3b+1 | 2a-b | 10a-5b | 4a-2b | 1-2a+b | 6a-3b |
分析 (1)根据题意可以得到d(103)和d(10-2)的值;
(2)根据d(mn)=d(m)+d(n),d( $\frac{m}{n}$)=d(m)-d(n),可以解答本题;
(3)先假设d(2)是正确的,可以得到d(4)和d(8)的值,然后和表格中的数据对照,从而可以解答本题.
解答 解:(1)∵d(10)=1,d(102)=2,
∴d(103)=3,d(10-2)=-2,
故答案为:3,-2;
(2)由题意可得,
$\frac{d({a}^{3})}{d(a)}=d({a}^{3})-d(a)$=d(a)+d(a)+d(a)-d(a)=2d(a),
∵d(3)=0.4771,
∴d(9)=d(32)=2d(3)=2×0.4771=0.9542,d($\frac{3}{10}$)=d(3)-d(10)=0.4771-1=-0.5229;
故答案为:2d(a),0.9542,-0.5229;
(3)x=0.8和x=3.2对应的d(x)错误,
理由:若d(2)=2a-b正确,
则d(4)=d(22)=2d(2)=2×(2a-b)=4a-2b,
d(8)=d(23)=3d(2)=3×(2a-b)=6a-3b,
故题目中的d(4)与d(8)正确,
∵表中与数x对应的劳格数d(x)有且只有两个是错误的,
∴d(2)的假设是正确的,
则d(0.8)=$d(\frac{8}{10})=d(8)-d(10)$=3d(2)-1=3×(2a-b)-1=6a-3b-1,故表格中的d(0.8)是错误的,
d(3.2)=$d(\frac{32}{10})=d(32)-d(10)=5d(2)-1$=5(2a-b)-1=10a-5b-1,故表格中的d(3.2)是错误的,
d(5)=$d(\frac{10}{2})=d(10)-d(2)$=1-(2a-b)=1-2a+b,故表格中的d(5)是正确的,
由上可得,表格中的d(0.8),d(3.2)是错误的,正确的d(0.8)=6a-3b-1,d(3.2)=10a-5b-1.
点评 本题考查整式的混合运算,解题的关键是明确题意,运用题目中的新定义解答问题.

 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:| 计算次数 | 计算结果 |
| 1 | -2 |
| 2 | 4 |
| 3 | 28 |
 将右边图形绕直线旋转一周,所得的立体图形是( )
将右边图形绕直线旋转一周,所得的立体图形是( )| A. |  | B. |  | C. |  | D. |  |
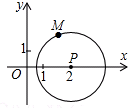 如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.
如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.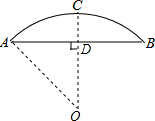 如图所示,已知AB=16m,半径OA=10m,高度CD为4m.
如图所示,已知AB=16m,半径OA=10m,高度CD为4m.