题目内容
19.设a、b、c都是正实数,且$\frac{a}{b}$$+\frac{b}{c}+\frac{c}{a}$=3,求证:a=b=c.分析 等式两边同乘abc,移项、提公因式把等式变形,解答即可.
解答 解:∵$\frac{a}{b}$$+\frac{b}{c}+\frac{c}{a}$=3,
∴a2c+b2a+c2b=3abc,
∴ac(a-b)+ba(b-c)+bc(c-a)=0,
∵a、b、c都是正实数,
∴a-b=0,b-c=0,c-a=0,
∴a=b=c.
点评 本题考查的是分式的混合运算,掌握分式的混合运算法则是解题的关键.

练习册系列答案
相关题目
1.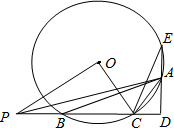 如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
(1)若∠ACB=120°,求证:CE=⊙O的半径.
(2)连OC,OP⊥OC交CB的延长线于P,若⊙O的半径为5cm,弦BC=6cm,求PB的长.
 如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E(1)若∠ACB=120°,求证:CE=⊙O的半径.
(2)连OC,OP⊥OC交CB的延长线于P,若⊙O的半径为5cm,弦BC=6cm,求PB的长.
5. 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:| 计算次数 | 计算结果 |
| 1 | -2 |
| 2 | 4 |
| 3 | 28 |
6.如果x2-kxy+4y2是关于x、y的完全平方式,那么k的值是( )
| A. | 2 | B. | 4 | C. | -4 | D. | 4或-4 |
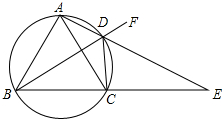 如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.
如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.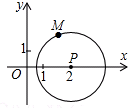 如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.
如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.