题目内容
17. 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒,t为何值时,DP⊥AC.
分析 (1)根据矩形的性质可得CD∥AB,根据平行线的性质可得∠DCQ=∠QAP,∠PDC=∠QPA,进而可得判定△APQ∽△CDQ;
(2)首先证明△ADQ∽△ACD,根据相似三角形的性质可得$\frac{AD}{AC}$=$\frac{AQ}{AD}$,然后计算出AC长,进而可得AQ长,再证明△AQP∽△ABC,可得$\frac{AQ}{AP}$=$\frac{AB}{AC}$,则$\frac{2\sqrt{5}}{t}$=$\frac{20}{10\sqrt{5}}$,再解即可得到t的值.
解答 (1)证明:∵四边形ABCD是矩形,
∴CD∥AB,
∴∠DCQ=∠QAP,∠PDC=∠QPA,
∴△APQ∽△CDQ;
(2)解:当t=5时,DP⊥AC;
∵∠ADC=90°,DP⊥AC,
∴∠AQD=∠AQP=∠ADC=90°,
∵∠DAQ=∠CAD,
∴△ADQ∽△ACD,
∴$\frac{AD}{AC}$=$\frac{AQ}{AD}$,
AC=$\sqrt{1{0}^{2}+2{0}^{2}}$=10$\sqrt{5}$,
则AQ=$\frac{A{D}^{2}}{AC}$=$\frac{1{0}^{2}}{10\sqrt{5}}$=2$\sqrt{5}$,
∵∠AQP=∠ABC=90°,∠QAP=∠BAC,
∴△AQP∽△ABC,
∴$\frac{AQ}{AP}$=$\frac{AB}{AC}$,
则$\frac{2\sqrt{5}}{t}$=$\frac{20}{10\sqrt{5}}$,
解得:t=5,
即当t=5时,DP⊥AC.
点评 此题主要考查了相似三角形的判定和性质,关键是掌握有两个角对应相等的三角形相似,相似三角形对应边成比例.

练习册系列答案
相关题目
5. 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:| 计算次数 | 计算结果 |
| 1 | -2 |
| 2 | 4 |
| 3 | 28 |
2.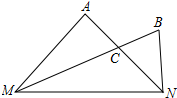 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )| A. | 若α=β,则点C在MN的垂直平分线上 | |
| B. | 若α+β=180°,则∠AMB=∠NMB | |
| C. | ∠MCN=$(\frac{α+β}{3}+60)$° | |
| D. | 当∠MCN=120°时,延长MA、NB交于点O,则OA=OB |
9. 将右边图形绕直线旋转一周,所得的立体图形是( )
将右边图形绕直线旋转一周,所得的立体图形是( )
 将右边图形绕直线旋转一周,所得的立体图形是( )
将右边图形绕直线旋转一周,所得的立体图形是( )| A. |  | B. |  | C. |  | D. |  |
6.如果x2-kxy+4y2是关于x、y的完全平方式,那么k的值是( )
| A. | 2 | B. | 4 | C. | -4 | D. | 4或-4 |
7.若代数式a2-2ab=7,那么代数式3ab-$\frac{3}{2}$a2-2的值是( )
| A. | $\frac{17}{2}$ | B. | 5 | C. | -$\frac{17}{2}$ | D. | -$\frac{25}{2}$ |
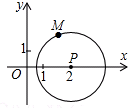 如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.
如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.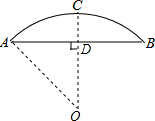 如图所示,已知AB=16m,半径OA=10m,高度CD为4m.
如图所示,已知AB=16m,半径OA=10m,高度CD为4m.