题目内容
1.为了抓住我市旅游文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过7650元,A纪念品的数量不少于50个,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
分析 (1)设购进A种纪念品每件价格为m元,B种纪念币每件价格为n元,根据题意得出关于m和n的二元一次方程组,解方程组即可得出结论;
(2)设购进A种纪念品x件,根据题意列出关于x的一元一次不等式组,解不等式组得出x的取值范围,即可得出结论;
(3)找出总利润关于购买A种纪念品x件的函数关系式,由函数的单调性确定总利润取最值时x的值,从而得出结论.
解答 解:(1)设购进A种纪念品每件价格为m元,B种纪念币每件价格为n元,根据题意可知:
$\left\{\begin{array}{l}{8m+3n=950}\\{5m+6n=800}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=100}\\{n=50}\end{array}\right.$.
答:购进A种纪念品每件需要100元,B种纪念品每件需要50元.
(2)设购进A种纪念品x件,则购进B种纪念品100-x件,根据题意可得:
$\left\{\begin{array}{l}{x≥50}\\{100x+50(100-x)≤7650}\end{array}\right.$,解得:50≤x≤53.
故该商店共有4种进货方案:A种50件,B种50件;A种51件,B种49件;A种52件,B种48件;A种53件,B种47件.
(3)销售总利润为20x+30(100-x)=3000-10x.
由总利润是关于x单调递减的函数可知:
当x=50时,获得利润最大,最大利润=3000-10×50=2500(元).
答:当购进A种纪念品50件,B种纪念品50件时,获得的利润最大,最大利润是2500元.
点评 本题考查了解二元一次方程组、解一元一次不等式组以及一次函数的性质,解题的关键:(1)列出关于两种纪念品单价的二元一次方程组;(2)列出关于购买A种纪念品件数x的一元一次不等式组;(3)根据一次函数的性质确定最值.本题属于中档题,难度不大,但考到的知识点稍多,解决该类题型时,明确解题的方法是关键,通过审题确定解题思路才能更快捷的解决该类问题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案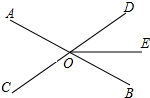 如图,直线AB、CD相交于点O,OE平分∠BOD,若∠AOD=2∠DOB,则∠EOB=30°.
如图,直线AB、CD相交于点O,OE平分∠BOD,若∠AOD=2∠DOB,则∠EOB=30°.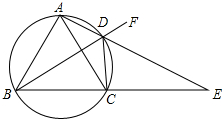 如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.
如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.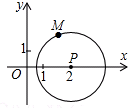 如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.
如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.