题目内容
18. 如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是①③④(填代号).
如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是①③④(填代号).①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.
分析 由AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,得出各相等的边角,再依据全等三角形的判定定理即可判定五个答案哪个一定成立.
解答 解:∵AB=AC,
∴∠EBC=∠DCB,
又∵BD平分∠ABC,∠CE平分∠ACB,
∴∠DBC=∠ECB,
∵∠BEC=180°-∠EBC-∠ECB,∠CDB=180°-∠DCB-∠DBC,
∴∠BEC=∠CDB.
在△EBC和△DCB中,$\left\{\begin{array}{l}{∠EBC=∠DCB}\\{∠BEC=∠CDB}\\{BC=CB}\end{array}\right.$,
∴△EBC≌△DCB(AAS).
即①成立;
在△BAD和△BCD中,仅有$\left\{\begin{array}{l}{∠CBD=∠ABD}\\{BD=BD}\end{array}\right.$,
不满足全等的条件,
即②不一定成立;
∵△EBC≌△DCB,
∴BD=CE.
在△BDA和△CEA中,$\left\{\begin{array}{l}{BD=CE}\\{∠A=∠A}\\{AB=AC}\end{array}\right.$,
∴△BDA≌△CEA(SAS).
即③成立;
∵△BDA≌△CEA,
∴AD=AE,
∵AB=AC,
∴BE=CD.
在△BOE和△COD中,$\left\{\begin{array}{l}{∠BEO=∠CDO}\\{∠EOB=∠DOC}\\{BE=CD}\end{array}\right.$,
∴△BOE≌△COD(AAS).
即④成立;
在△ACE和△BCE中,仅有$\left\{\begin{array}{l}{∠ACE=∠BCE}\\{CE=CE}\end{array}\right.$,
不满足全等的条件,
即⑤不一定成立.
综上可知:一定成立的有①③④.
故答案为:①③④.
点评 本题考查了全等三角形的判定及性质、角平分线的定义即等腰三角形的性质,解题的关键是找出各边角关系,利用全等三角形的判定定理去寻找全等三角形.本题属于中档题,难度不大,在解决该类题型中,不妨结合图形与已知知识直接判定.

 将右边图形绕直线旋转一周,所得的立体图形是( )
将右边图形绕直线旋转一周,所得的立体图形是( )| A. |  | B. |  | C. |  | D. |  |
| A. | 2 | B. | 4 | C. | -4 | D. | 4或-4 |
| A. | $\frac{17}{2}$ | B. | 5 | C. | -$\frac{17}{2}$ | D. | -$\frac{25}{2}$ |
 如图:一次函数y=kx+b的图象经过A、B两点,则不等式kx+b>0的解集是( )
如图:一次函数y=kx+b的图象经过A、B两点,则不等式kx+b>0的解集是( )| A. | x>0 | B. | x>2 | C. | x>-3 | D. | -3<x<2 |
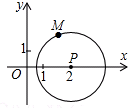 如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.
如图,以点P(2,0)为圆心,$\sqrt{3}$为半径作圆,点M(a,b) 是⊙P上的一点,设$\frac{b}{a}$=t,则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$.