题目内容
5.在实数范围内分解因式(1)x4-9
(2)y2-2$\sqrt{3}$y+3.
分析 (1)首先利用平方差进行分解,再利用平方差进行二次分解;
(2)直接利用完全平方公式进行分解即可.
解答 解:(1)原式=(x2+3)(x2-3)=(x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$);
(2)原式=(y-$\sqrt{3}$)2.
点评 此题主要考查了实数范围内分解因式,关键是掌握完全平方公式和平方差公式.

练习册系列答案
相关题目
17.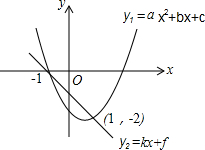 若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
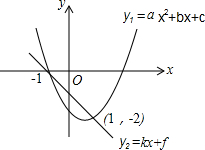 若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )| A. | $\left\{\begin{array}{l}{mx<1}\\{nx>1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{mx>1}\\{nx>1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{mx>1}\\{nx<1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{mx<1}\\{nx<1}\end{array}\right.$ |
14.计算a5•(-$\frac{1}{a}$)2的结果是( )
| A. | -a3 | B. | a3 | C. | a7 | D. | a10 |
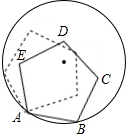 如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为12°.
如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为12°.