题目内容
15.一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球处颜色外都相同,将球搅匀,从中任意摸出1个球.(1)会出现哪些可能的结果?
(2)能够确定摸到的一定是红球吗?
(3)你认为摸到哪种颜色的球可能性最大?哪种颜色的球可能性最小?
(4)怎样改变袋子中红球、绿球和白球的个数,使摸到这三种颜色的球的概率相同?
分析 (1)由一只不透明的袋子中有2个红球、3个绿球和5个白球,即可求得答案;
(2)由随机事件的意义可求得答案;
(3)由一只不透明的袋子中有2个红球、3个绿球和5个白球,即可知摸到哪种颜色的球可能性最大?哪种颜色的球可能性最小?
(4)将袋子中的红球、绿球与白球的个数设计一样多,则摸到这三种颜色的球的概率相同.
解答 解:(1)∵一只不透明的袋子中有2个红球、3个绿球和5个白球,
∴会出现可能的结果有:红球、绿球、白球;
(2)不能;
(3)摸到白球可能性最大,红球可能性最小;
(4)将袋子中的红球、绿球与白球的个数设计一样多,则摸到这三种颜色的球的概率相同.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
6.如果将长为8cm,宽为6cm的矩形纸片折叠一次,那么这条折痕的长不可能是( )
| A. | 7cm | B. | 8cm | C. | 10cm | D. | 11cm |
3.有五张质地、大小、反面完全相同的不透明卡片,正面分别写着数字1,2,3,4,5,现把它们的正面向下,随机摆放在桌面上,从中任意抽出一张,则抽出的数字是奇数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
10.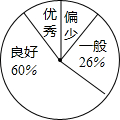 某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
请根据以上信息回答下列问题:
(1)求出本次随机抽取的学生总人数;
(2)分别求出统计表中的x,y的值;
(3)估计该校九年级400名学生中为“优秀”档次的人数.
 某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:| 阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
(1)求出本次随机抽取的学生总人数;
(2)分别求出统计表中的x,y的值;
(3)估计该校九年级400名学生中为“优秀”档次的人数.
4.从一块半径是4m的圆形铁片上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )
| A. | $\sqrt{2}$m | B. | 2m | C. | 4m | D. | $\sqrt{15}$m |
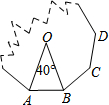 如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=9.
如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=9.