题目内容
17.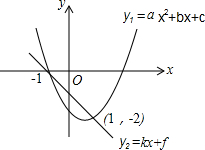 若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )| A. | $\left\{\begin{array}{l}{mx<1}\\{nx>1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{mx>1}\\{nx>1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{mx>1}\\{nx<1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{mx<1}\\{nx<1}\end{array}\right.$ |
分析 根据二次函数与不等式(组)的关系,结合图象,得出y1<y2时,x的取值范围是-1<x<1;再找到不等式组中解为-1<x<1的选项,即可求解.
解答  解:由图形可以看出:
解:由图形可以看出:
抛物线y1=ax2+bx+c和一次函数y2=kx+f(k≠0)的交点横坐标分别为-1,1,
当y1<y2时,x的取值范围正好在两交点之间,即-1<x<1.
A、mn<0,该方程组的解集为x<$\frac{1}{n}$<0,故本选项错误;
B、mn<0,该方程组的解集为x<$\frac{1}{m}$<0故本选项错误;
C、mn<0,该方程组的解集为x>$\frac{1}{m}$>0,故本选项错误;
D、mn<0,该方程组的解集为$\frac{1}{n}$<x$<\frac{1}{m}$(n<0<m)或$\frac{1}{n}$>x>$\frac{1}{m}$(m<0<n),故本选项正确.
故选:D.
点评 本题考查了二次函数与不等式(组).此类题可用数形结合的思想进行解答,这也是速解习题常用的方法.

练习册系列答案
相关题目
6.如果将长为8cm,宽为6cm的矩形纸片折叠一次,那么这条折痕的长不可能是( )
| A. | 7cm | B. | 8cm | C. | 10cm | D. | 11cm |
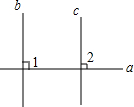 如图,已知a⊥b,a⊥c,求证:b∥c.
如图,已知a⊥b,a⊥c,求证:b∥c.
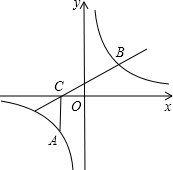 如图,点A为双曲线y=$\frac{k}{x}$(k>0)上一点,AC⊥x轴于C,过C的直线l交双曲线于B,∠BCO=30°,BC=2$\sqrt{3}$,点A横坐标为-1.
如图,点A为双曲线y=$\frac{k}{x}$(k>0)上一点,AC⊥x轴于C,过C的直线l交双曲线于B,∠BCO=30°,BC=2$\sqrt{3}$,点A横坐标为-1.