题目内容
13.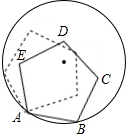 如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为12°.
如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为12°.
分析 因为点E旋转的角度和点C旋转的角度相等,所以求出点E旋转的角度即可.
解答 解: 如图设圆心为O,连接OA、OB,点E落在圆上的点E′处.
如图设圆心为O,连接OA、OB,点E落在圆上的点E′处.
∵AB=OA=OB,
∴∠OAB=60°,同理∠OAE′=60°,
∵∠EAB=108°,
∴∠EAO=∠EAB-∠OAB=48°,
∴∠EAE′=∠OAE′-∠EAO=60°-48°=12°,
∵点E旋转的角度和点C旋转的角度相等,
∴点C旋转的角度为12°,
故答案为12°.
点评 本题考查正多边形与圆,旋转的性质,理解点E旋转的角度和点C旋转的角度相等是解决问题的关键,所以中考常考题型.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
3.下列各式由左到右的变形中,属于因式分解的是( )
| A. | (x+2)(x-1)=x2+x-2 | B. | x2+x+1=(x+1)2-x | ||
| C. | -a2-ab-ac=-a(a+b+c ) | D. | a2+b2=(a+b)2-2ab |
4.已知∠1与∠2是直线a与直线b被直线c所截得的内错角,且有∠1=50°,则∠2=( )
| A. | 130° | B. | 50° | C. | 80° | D. | 无法确定 |
3.有五张质地、大小、反面完全相同的不透明卡片,正面分别写着数字1,2,3,4,5,现把它们的正面向下,随机摆放在桌面上,从中任意抽出一张,则抽出的数字是奇数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
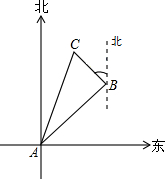 如图,在一次实践活动中,小强从A地出发,沿北偏东60°的方向行进3$\sqrt{3}$千米到达B地,然后再沿北偏西30°方向行进了3千米到达目的地C.
如图,在一次实践活动中,小强从A地出发,沿北偏东60°的方向行进3$\sqrt{3}$千米到达B地,然后再沿北偏西30°方向行进了3千米到达目的地C.