题目内容
15.阅读下列材料,若要比较代数式a与b的大小.我们可以利用不等式的性质来说明.例加:若a-b>0,则a>b;
若a-b=0,则a=b;
若a-b<0,则a<b.
像上述比较两个代数式大小的方法叫做作差法.作差法是比较两个代数式的大小的一种常用的方法.也是一种很有效的方法.利用上述堤供的信息.试比较a2(a-b)与b2(b-a)的大小.
分析 根据题意利用作差法比较两式子的大小即可.
解答 解:∵a2(a-b)-b2(b-a)=(a-b)(a2+b2),
∴当a>b时,a-b>0,a2+b2>0,
∴a2(a-b)>b2(b-a);
当a=b时,a-b=0,
∴a2(a-b)=b2(b-a);
当a<b时,a-b<0,a2+b2>0,
∴a2(a-b)<b2(b-a).
点评 本题考查的是不等式的性质,在解答此类题目时要注意进行分类讨论,不要漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.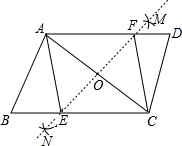 如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
 如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )| A. | AE=AF | B. | AC=EF | C. | ∠EAF=90° | D. | ∠AFE=45° |
3.下列各式由左到右的变形中,属于因式分解的是( )
| A. | (x+2)(x-1)=x2+x-2 | B. | x2+x+1=(x+1)2-x | ||
| C. | -a2-ab-ac=-a(a+b+c ) | D. | a2+b2=(a+b)2-2ab |
10.分式方程$\frac{2}{x}$=$\frac{3}{x+2}$的解为( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=1 |
20.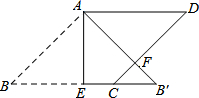 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2$-\sqrt{2}$ | D. | 2$\sqrt{2}$-2 |
4.已知∠1与∠2是直线a与直线b被直线c所截得的内错角,且有∠1=50°,则∠2=( )
| A. | 130° | B. | 50° | C. | 80° | D. | 无法确定 |
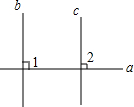 如图,已知a⊥b,a⊥c,求证:b∥c.
如图,已知a⊥b,a⊥c,求证:b∥c.