题目内容
3.下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.(-x2+3xy-$\frac{1}{2}$y2)-(-$\frac{1}{2}$x2+4xy-$\frac{3}{2}$y2)=-$\frac{1}{2}$x2 +y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )| A. | -7xy | B. | +7xy | C. | -xy | D. | +xy |
分析 根据题意得出整式相加减的式子,再去括号,合并同类项即可.
解答 解:由题意得,被墨汁遮住的一项=(-x2+3xy-$\frac{1}{2}$y2)-(-$\frac{1}{2}$x2+4xy-$\frac{3}{2}$y2)-(-$\frac{1}{2}$x2+y2)
=-x2+3xy-$\frac{1}{2}$y2+$\frac{1}{2}$x2-4xy+$\frac{3}{2}$y2+$\frac{1}{2}$x2-y2
=-xy.
故选C.
点评 本题考查的是整式的加减,熟知整式的加减实质上是合并同类项是解答此题的关键.

练习册系列答案
相关题目
13.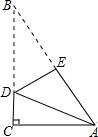 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
14.一个六边形,每一个内角都相等,每个内角的度数为( )
| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
11.下列命题中,逆命题成立的是( )
| A. | 两个全等三角形的对应角相等 | |
| B. | 如果两个实数是正数,那么它们的积是正数 | |
| C. | 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形 | |
| D. | 如果两个角是直角,那么它们相等 |
18.下列图形中,由∠1=∠2,能使AB∥CD成立的是( )
| A. |  | B. |  | C. |  | D. |  |