题目内容
13.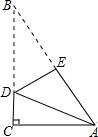 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
分析 利用特殊角度构成特殊三角形,运用三角函数求解.
解答 解:由折叠的性质可得,点E是等腰三角形DAB的底边上的中点.
根据等腰三角形的性质知,DE⊥AB.
∵∠B=30°,AC=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,BE=$\sqrt{3}$.
∴DE=BEtan30°=1.
故选C.
点评 此题考查折叠问题,关键是利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②等腰三角形的判定和性质,锐角三角函数的概念求解.

练习册系列答案
相关题目
5. 将图中所示的图案平移后得到的图案是( )
将图中所示的图案平移后得到的图案是( )
 将图中所示的图案平移后得到的图案是( )
将图中所示的图案平移后得到的图案是( )| A. |  | B. |  | C. |  | D. |  |
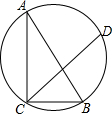 如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).
如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).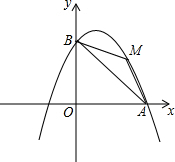 如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.
如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C. +y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )