题目内容
17.先化简,再求值(1)(x+2)2-(x+5)(x-5),其中x=$\frac{3}{2}$.
(2)[(x+2y)2-(x+y)(3x-y)-5y2]÷2x,其中x=-2,y=$\frac{1}{2}$.
分析 (1)原式利用完全平方公式,平方差公式化简,去括号合并得到最简结果,把x的值代入计算即可求出值;
(2)原式中括号中利用完全平方公式,平方差公式化简,去括号合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=x2+4x+4-x2+25=4x+29,
当x=$\frac{3}{2}$时,原式=6+29=35;
(2)原式=(x2+4xy+4y2-3x2+xy-3xy+y2-5y2)÷2x=(-2x2+2xy)÷2x=-x+y,
当x=-2,y=$\frac{1}{2}$时,原式=2+$\frac{1}{2}$=2.5.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
2.多项式(x+2)(2x-1)-2(x+2)可以因式分解成(x+m)(2x+n),则m-n的值是( )
| A. | 2 | B. | -2 | C. | 4 | D. | 5 |
9.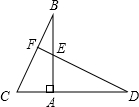 如图,已知Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转,使点D落在射线CA上,DE的延长线交BC于F,则∠CFD的度数为( )
如图,已知Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转,使点D落在射线CA上,DE的延长线交BC于F,则∠CFD的度数为( )
 如图,已知Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转,使点D落在射线CA上,DE的延长线交BC于F,则∠CFD的度数为( )
如图,已知Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转,使点D落在射线CA上,DE的延长线交BC于F,则∠CFD的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 120° |