Question

9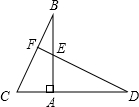．如图，已知Rt△ABC中，∠BAC=90°，将△ABC绕点A顺时针旋转，使点D落在射线CA上，DE的延长线交BC于F，则∠CFD的度数为（　　）

• A． 80°
• B． 90°
• C． 100°
• D． 120°

Answer 1

分析 根据旋转的性质得出全等，推出∠B=∠D，求出∠B+∠BEF=∠D+∠AED=90°，根据三角形外角性质得出∠CFD=∠B+∠BEF，代入求出即可．

解答 解：∵将△ABC绕点A顺时针旋转得到△ADE，
∴△ABC≌△ADE，
∴∠B=∠D，
∵∠CAB=∠BAD=90°，∠BEF=∠AED，∠B+∠BEF+∠BFE=180°，∠D+∠BAD+∠AED=180°，
∴∠B+∠BEF=∠D+∠AED=180°-90°=90°，
∴∠CFD=∠B+∠BEF=90°，
故选：B．

点评 本题考查了旋转的性质，全等三角形的性质和判定，三角形内角和定理，三角形外角性质的应用，掌握旋转变换的性质是解题的关键．