题目内容
1.我们定义:只有一组对角相等的凸四边形叫做等对角四边形.(1)四边形ABCD是等对角四边形,∠A≠∠C,若∠A=70°,∠B=80°,则∠C=130°,∠D=80°.
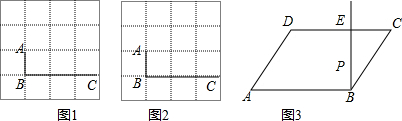
(2)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在格点上,按要求以AB、BC为边在图①、图②中各画一个等对角四边形ABCD.要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.
(3)如图③,在?ABCD中,∠A=60°,AB=5,AD=4,BE⊥DC于点E.点P在射线BE上,设BP=x,求四边形ABPD为等对角四边形时x的值.
分析 (1)由等对角四边形得出∠B=∠D,再由四边形内角和即可求出∠C;
(2)连接BD,由AB=AD,得出∠ABD=∠ADB,证出∠CBD=∠CDB,即可得出CB=CD;
(3)过点D作DH⊥AB于点H,则四边形DHBE为矩形,根据三角函数求出AH和HD,分两种情况进行讨论,①当∠ADP=∠ABP=90°时;②当∠DPB=∠A=60°时,即可得出答案.
解答 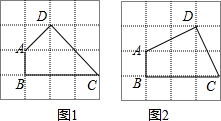 解:(1)∵四边形ABCD是“等对角四边形”,∠A≠∠C,
解:(1)∵四边形ABCD是“等对角四边形”,∠A≠∠C,
∴∠D=∠B=80°,
∴∠C=360°-∠A-∠B-∠D=360°-70°-80°-80°=130°;
故答案为:130,80;
(2)如图所示,
(3)过点D作DH⊥AB于点H,则四边形DHBE为矩形,
∴DE=BH,BE=DH,
∵∠A=60°,∠DHA=90°,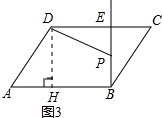
∴AH=AD•cos60°=4×$\frac{1}{2}$=2,
DH=AD•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴BE=DH=2$\sqrt{3}$,BH=AB-AH=5-2=3,
∴DE=BH=3,
如图3,当∠ADP=∠ABP=90°时,∠BPD=120°,
∴∠DPE=180°-∠BPD=60°,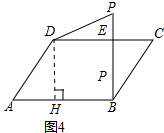
又∵∠DEP=90°,
∴PE=$\frac{DE}{tan60°}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴x=BE-EP=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$;
如图4,当∠DPB=∠A=60°时,
∵∠P=60°,∠PED=90°,
∴PE=DE•cot60°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∴BP=BE+PE=2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$.
综上,当四边形ABPD为等对角四边形时x的值为$\sqrt{3}$或3$\sqrt{3}$.
点评 本题是四边形综合题目,考查了新定义、四边形内角和定理、等腰三角形的判定与性质、勾股定理、三角函数、矩形的判定与性质等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,通过作辅助线运用三角函数和勾股定理才能得出结果.

 如图,AB是⊙O的直径,弦CO⊥AB,∠C=30°,CD=24,则阴影部分的面积是( )
如图,AB是⊙O的直径,弦CO⊥AB,∠C=30°,CD=24,则阴影部分的面积是( )| A. | 32π | B. | 16π | C. | 16 | D. | 32 |
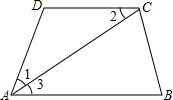 如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.
如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.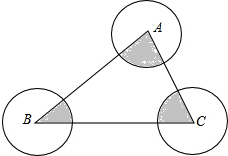 ⊙A、⊙B、⊙C两两不相交,且半径都是0.5cm,则图中的三个扇形(即阴影部分)的面积之和为$\frac{π}{8}$cm2.
⊙A、⊙B、⊙C两两不相交,且半径都是0.5cm,则图中的三个扇形(即阴影部分)的面积之和为$\frac{π}{8}$cm2. 如图,CD是∠ACB的平分线,∠EDC=25°,∠A=60°,∠B=70°,
如图,CD是∠ACB的平分线,∠EDC=25°,∠A=60°,∠B=70°,