题目内容
13. 如图,CD是∠ACB的平分线,∠EDC=25°,∠A=60°,∠B=70°,
如图,CD是∠ACB的平分线,∠EDC=25°,∠A=60°,∠B=70°,(1)证明:DE∥BC;
(2)求∠BDC的度数.
分析 (1)先根据三角形内角和定理求出∠ACB的度数,再由角平分线的性质求出∠ACD与∠BCD的度数,进而可得出结论;
(2)根据(1)中∠BCD的度数即可得出结论.
解答 (1)证明:∵∠A=60°,∠B=70°,
∴∠ACB=180°-60°-70°=50°.
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD=25°.
∵∠EDC=25°,
∴∠EDC=∠BCD,
∴DE∥BC;
(2)∵∠B=70°,∠BCD=25°,
∴∠BDC=180°-70°-25°=85°.
点评 本题考查的是平行线的判定定理,用到的知识点为:内错角相等,两直线平行.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
18.下列命题中假命题是( )
| A. | 两边及第三边上的高对应相等的两个三角形全等 | |
| B. | 两边及第三边上的中线对应相等的两个三角形全等 | |
| C. | 两边及两边的夹角对应相等的两个三角形全等 | |
| D. | 两边及其中一边上的中线对应相等的两个三角形全等 |
 如图,AB为⊙O的直径,点C是⊙O上一点,BD切⊙O于点B,交AC的延长线于点D,点E为$\widehat{AC}$的中点,连接BE交AC于点F.
如图,AB为⊙O的直径,点C是⊙O上一点,BD切⊙O于点B,交AC的延长线于点D,点E为$\widehat{AC}$的中点,连接BE交AC于点F.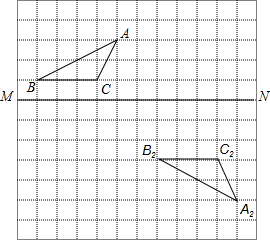 在如图所示的方格纸中.
在如图所示的方格纸中.