题目内容
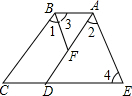
11.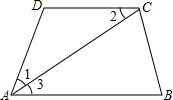 如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.
如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.证明:∵AC平分∠DAB(已知)
∴∠1=∠3(角平分线定义)
又∵∠1=∠2(已知)
∴∠2=∠3(等量替换)
∴AB∥CD(内错角相等两直线平行)
分析 根据证明平行线的方法,一步步的补充完整证明过程,即可得出结论.
解答 证明::∵AC平分∠DAB(已知)
∴∠1=∠3(角平分线定义)
又∵∠1=∠2(已知)
∴∠2=∠3(等量替换)
∴AB∥CD(内错角相等两直线平行).
故答案为:已知;3;平行线的定义;已知;3;等量代换;CD;内错角相等两直线平行.
点评 本题考查了平行线的判定,解题的关键是能够根据内错角相等证出两直线平行.本题属于基础题,难度不大,解决该题型题目时,根据平行线的判定定理去寻找相等(或互补)的角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.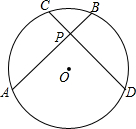 如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
 如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )| A. | $\widehat{AC}$=$\widehat{BD}$ | B. | $\widehat{AC}$$>\widehat{BD}$ | C. | $\widehat{AC}$$<\widehat{BD}$ | D. | 不能确定 |
2.在?ABCD中,∠D、∠C的度数之比为3:1,则∠A等于( )
| A. | 45° | B. | 135° | C. | 50° | D. | 130° |
 如图,己知∠1=∠2,∠3=∠4,CE∥AB,试说明:AD∥BC.
如图,己知∠1=∠2,∠3=∠4,CE∥AB,试说明:AD∥BC.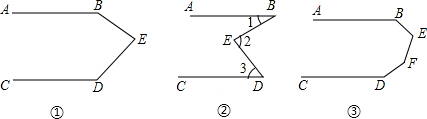
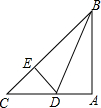 如图,△ABC是等腰直角三角形,∠A=90°,BD是角平分线,DE⊥BC,BC=20,则△DCE的周长为20.
如图,△ABC是等腰直角三角形,∠A=90°,BD是角平分线,DE⊥BC,BC=20,则△DCE的周长为20.