题目内容
4.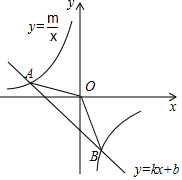 如图,已知A(-4,2)、B(a,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;
如图,已知A(-4,2)、B(a,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;(1)求一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.
分析 (1)由反比例函数图象上点的坐标特征可求出m、a的值,从而得出点B的坐标,根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)由两函数图象的上下位置关系结合交点的横坐标,即可得出使一次函数的值小于反比例函数的值的x的取值范围;
(3)设直线AB与y轴的交点为C,利用一次函数图象上点的坐标特征可求出点C的坐标,进而得出OC的长度,根据三角形的面积公式结合S△AOB=S△AOC+S△BOC即可求出△AOB的面积.
解答 解:(1)∵m=xy=(-4)×2=-8,
∴-4a=-8,
∴a=2,
∴B(2,-4).
将A(-4,2)、B(2,-4)代入y=kx+b,
$\left\{\begin{array}{l}{2=-4k+b}\\{-4=2k+b}\end{array}\right.$,解得:$\left\{{\begin{array}{l}{k=-1}\\{b=-2}\end{array}}\right.$,
∴一次函数的解析式为y=-x-2.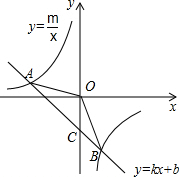
(2)观察函数图象可知:当-4<x<0或x>2时,一次函数图象在反比例函数图象下方,
∴一次函数的值小于反比例函数值的x的取值范围:-4<x<0或x>2.
(3)设直线AB与y轴的交点为C,如图所示.
当x=0时,y=-x-2=-2,
∴C(0,-2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$OC•|xA|+$\frac{1}{2}$OC•|xB|=$\frac{1}{2}$×2×4+$\frac{1}{2}$×2×2=6.
点评 本题考查了待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)根据点的坐标利用待定系数法求出一次函数解析式;(2)根据两函数图象的上下位置关系找出使一次函数的值小于反比例函数的值的x的取值范围;(3)利用分割图形求面积法求出△AOB的面积.


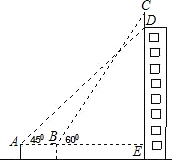 如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)
如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)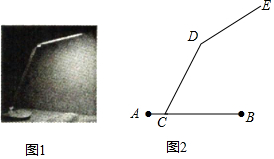 如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)
如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)