题目内容
9.已知在平面直角坐标系中,点A、B、C、D的坐标依次为(-1,0),(m,n),(-1,10),(-9,p),且p≤n.若以A、B、C、D四个点为顶点的四边形是菱形,则n的值是4或5或18.分析 利用菱形的性质结合A,C点坐标进而得出符合题意的n的值.
解答 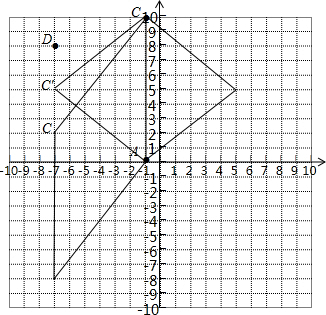 解:如图所示:当C(-9,2),C′(-9,5)时,都可以得到以A、B、C、D四个点为顶点的四边形是菱形,
解:如图所示:当C(-9,2),C′(-9,5)时,都可以得到以A、B、C、D四个点为顶点的四边形是菱形,
同理可得:当D(-9,8)则对应点C的坐标为;(-9,18)可以得到以A、B、C、D四个点为顶点的四边形是菱形,
故n的值为:4或5或18.
故答案为:4或5或18.
点评 此题主要考查了菱形的判定以及坐标与图形的性质,利用菱形的性质得出C点坐标是解题关键.

练习册系列答案
相关题目
18. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠CON=55°,则∠AOM的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠CON=55°,则∠AOM的度数为( )
 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠CON=55°,则∠AOM的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠CON=55°,则∠AOM的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
19.下列运算不正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | B. | a3+a4=a7 | C. | a6÷a3=a3 | D. | (3a3)2=9a6 |
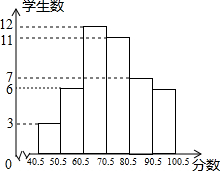 某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是80%.
某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是80%.
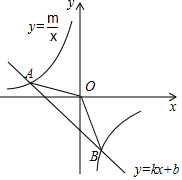 如图,已知A(-4,2)、B(a,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;
如图,已知A(-4,2)、B(a,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点; 甲、乙、丙、丁四位同学一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB,
甲、乙、丙、丁四位同学一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB,