题目内容
6.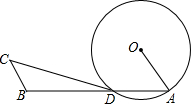 如图,点A、点D在⊙O上,0A=1,$\widehat{AD}$=$\frac{π}{2}$,点B在射线AD上,若BC∥OA,判断直线CD与⊙O的位置关系,并说明理由.
如图,点A、点D在⊙O上,0A=1,$\widehat{AD}$=$\frac{π}{2}$,点B在射线AD上,若BC∥OA,判断直线CD与⊙O的位置关系,并说明理由.
分析 连接OD,如图,可根据$\widehat{AD}$的长求出∠AOD,然后根据条件可推出∠ODC>90°,由此就可得到直线CD与⊙O的位置关系.
解答 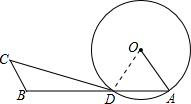 解:直线CD与⊙O相交.理由如下:
解:直线CD与⊙O相交.理由如下:
连接OD,如图,
∵l$\widehat{AD}$=$\frac{nπ×1}{180}$=$\frac{π}{2}$,
∴n=90,即∠AOD=90°.
∵OA=OD,
∴∠ODA=∠OAD=45°.
∵BC∥OA,
∴∠B+∠A=180°,
∴∠B=135°,
∴∠ADC>135°,
∵∠ODC>135°-45°=90°,
∴直线CD与⊙O不相切.
∵点D既在直线CD上,又在⊙O上,
∴直线CD与⊙O相交.
点评 本题主要考查了平行线的性质、三角形外角的性质、等腰三角形的性质、弧长公式、直线CD与⊙O的位置关系等知识,要判定直线CD与⊙O是否相切,只需判定∠ODC是否等于90°.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
15.下列叙述正确的是( )
| A. | 如果a存在平方根,则a>0 | B. | $\sqrt{16}$=±4 | ||
| C. | $\sqrt{5}$是5的一个平方根 | D. | 5的平方根是$\sqrt{5}$ |
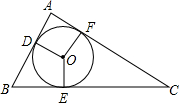 如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.
如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.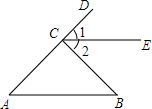 如图,已知∠A=∠B,点A,C,D在同一条直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,试说明CE∥AB.
如图,已知∠A=∠B,点A,C,D在同一条直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,试说明CE∥AB.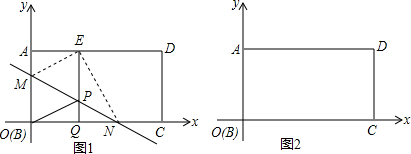
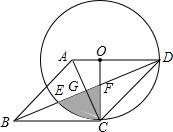 如图,已知菱形ABCD中,AD∥BC,AD=$\sqrt{2}$,点O是AD上一点,以O为圆心,OD长为半径的⊙O与BC相切于点C,与BD相交于点E,连接OC,AC,分别与BD相交于点F,G.
如图,已知菱形ABCD中,AD∥BC,AD=$\sqrt{2}$,点O是AD上一点,以O为圆心,OD长为半径的⊙O与BC相切于点C,与BD相交于点E,连接OC,AC,分别与BD相交于点F,G.