题目内容
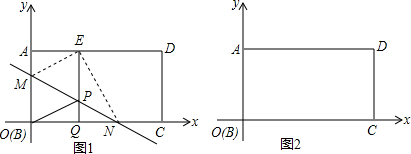
18.(Ⅰ)如图1,在平面直角坐标系xoy中,将矩形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB边放在y轴的正半轴上,AB=m,AD=n,(m≤n).将纸片折叠,使点B落在边AD上的点E处,过点E作EQ⊥BC于点Q,折痕MN所在直线与直线EQ相交于点P,连结OP. 求证:四边形OMEP是菱形;(Ⅱ)设点P坐标是(x,y),点P的轨迹称为折叠曲线,求y与x的函数关系式(用含m的代数式表示);
(Ⅲ)将矩形纸片ABCD如图2放置,AB=8,AD=12,将纸片折叠,当点B与点D重合时,折痕与DC的延长线交于点F.试问在这条折叠曲线上是否存在点K,使得△KCF的面积是△KOC面积的$\frac{5}{3}$?若存在,写出点K的坐标;若不存在,请说明理由.
分析 (Ⅰ)由折叠有,OM=ME,∠OMN=∠EMN,再判定出四边形OMEP是平行四边形,即可;
(Ⅱ)由菱形的性质得到,OP=PE,从而x2+y2=m2-2my+y2即可;
(Ⅲ)假设折叠曲线上存在点K满足条件,设出K的坐标,表示出S△KCF=$\frac{1}{2}$CF×KG=$\frac{1}{2}$×5×(12-x),S△KOC=$\frac{1}{2}$CO×KH=$\frac{1}{2}$×12×y,用S△KCF=$\frac{5}{3}$S△KOC建立方程,解得方程即可.
解答 (Ⅰ)证明:由折叠有,OM=ME,∠OMN=∠EMN,
∵OM∥EP,
∴∠OMN=∠MPE.
∴∠EMN=∠MPE.
∴ME=EP.
∴OM=EP.
∴四边形OMEP是平行四边形.
又∵ME=EP,
∴四边形OMEP是菱形.
(Ⅱ)∵四边形OMEP是菱形,
∴OP=PE∴OP2=PE2,
∵EQ=OA=m,PQ=y,
∴PE=m-y.
∴PE2=(m-y)2=m2-2my+y2.
∵OP2=x2+y2,PE2=m2-2my+y2,
∴x2+y2=m2-2my+y2.
∴y=-$\frac{1}{2m}$x2+$\frac{m}{2}$(0≤x≤m)
(Ⅲ)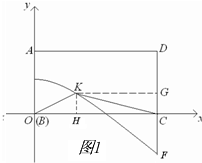
如图1,假设折叠曲线上存在点K满足条件.
当m=8时,y=-$\frac{1}{16}$x2+4,
作KG⊥DC于G,KH⊥OC于H.设K(x,y),
则KG=12-x,KH=y.
当x=12时,y=-5.
∴F(12,-5)
∴CF=5.
∴S△KCF=$\frac{1}{2}$CF×KG=$\frac{1}{2}$×5×(12-x),
S△KOC=$\frac{1}{2}$CO×KH=$\frac{1}{2}$×12×y,
∵S△KCF=$\frac{5}{3}$S△KOC,
∴$\frac{1}{2}$×5×(12-x)=$\frac{5}{3}$×$\frac{1}{2}$×12×y,
∴y=$\frac{12-x}{4}$.
∴K(x,$\frac{12-x}{4}$),
∵点K在y=-$\frac{1}{16}$x2+4,上,
∴$\frac{12-x}{4}$=-$\frac{1}{16}$x2+4.
∴x2-4x-16=0,
∴x1=2+2$\sqrt{5}$,x2=2-2$\sqrt{5}$(舍),
当x1=2+2$\sqrt{5}$,时,y=$\frac{5-\sqrt{5}}{2}$,
∴存在点K($2+2\sqrt{5}$,$\frac{{5-\sqrt{5}}}{2}$).
点评 此题是几何变换的综合题,主要考查平行四边形的性质,和平面坐标系中两点间的距离公式,用线段相等和面积关系建立方程是解本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
 如图,点A、点D在⊙O上,0A=1,$\widehat{AD}$=$\frac{π}{2}$,点B在射线AD上,若BC∥OA,判断直线CD与⊙O的位置关系,并说明理由.
如图,点A、点D在⊙O上,0A=1,$\widehat{AD}$=$\frac{π}{2}$,点B在射线AD上,若BC∥OA,判断直线CD与⊙O的位置关系,并说明理由.
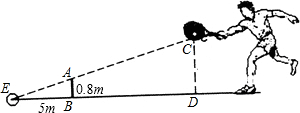 如图,小明打网球时能击中球的最高高度CD是2.4m,如果发球时要使球恰好能打过网AB,且落在离网5m的位置上,那么小明在离网多远的位置发球?
如图,小明打网球时能击中球的最高高度CD是2.4m,如果发球时要使球恰好能打过网AB,且落在离网5m的位置上,那么小明在离网多远的位置发球?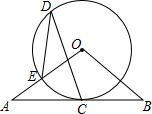 如图,AB与⊙O相切于点C,∠A=∠B,OA,OB分别交⊙O于点E,F.
如图,AB与⊙O相切于点C,∠A=∠B,OA,OB分别交⊙O于点E,F.