题目内容
11.已知A(-2,3),B(2,1),P点在x轴上,若PA+PB长度最小,则点P坐标为(1,0);若PA-PB长度最大,则点P坐标为(4,0).分析 找到B点关于x轴的对称点B′,连接AB′交x轴于点P,即可得到要求的P点,再根据一次函数的性质,找到各点的坐标,即可得出答案.根据三角形的性质,两边之差小于第三边,连接AB交x轴于点P,即可得到要求的P点.
解答 解:求最小值:如图所示: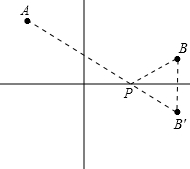 ,
,
作B点关于x轴的对称点B',连接AB′,交x轴于点P,
∵B和B′对称,
∴PB=PB′,
∴AP+BP=PA+B′P,
根据两点之间线段最短可知P点为所求.
∵已知A(-2,3),B(2,1),
∴B′坐标为(2,-1),
则可求得最短距离为AB′的长度,AB′=$\sqrt{(2+2)^{2}+(3+1)^{2}}=4\sqrt{2}$,
∴PA+PB长度最小,则最小值为4$\sqrt{2}$.
直线AB'的解析式为y=mx+n,
可得:$\left\{\begin{array}{l}{-2m+n=3}\\{2m+n=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-1}\\{n=1}\end{array}\right.$,
把y=0代入y=-x+1,可得:x=1,
所以点P的坐标为(1,0);
求最大值:如图所示: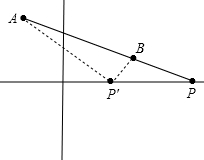 ,
,
连接AB并延长,交x轴于点P,
任取一点P',连接AP'、BP',
在△ABP'中,根据三角形的性质,两边之差小于第三边,
即AP'-BP'<AB,
∴可知AB为所求的最大值,
∵已知A(-2,3),B(2,1),
∴直线AB的解析式为y=ax+b,
可得:$\left\{\begin{array}{l}{-2a+b=3}\\{2a+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-0.5}\\{b=2}\end{array}\right.$,
把y=0代入y=-0.5x+2中,可得:x=4,
所以点P的坐标为(4,0).
故答案为:(1,0);(4,0).
点评 本题属于综合性的试题,包含了一次函数的应用、对称图形的性质、三角形的性质以及最大值最小值的求法.解决这类题目要求对于所学的各种知识点要能够融会贯通,达到“信手拈来”的地步.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | a | B. | -a | C. | ±a | D. | |a| |
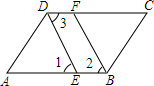 如图.∠1=∠2,∠2=∠3.你能判断图中哪些直线平行.并说明理由.
如图.∠1=∠2,∠2=∠3.你能判断图中哪些直线平行.并说明理由.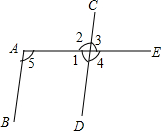 如图,写出所有能使AB∥CD的条件,并写出相应的根据.
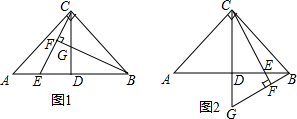
如图,写出所有能使AB∥CD的条件,并写出相应的根据.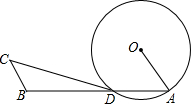 如图,点A、点D在⊙O上,0A=1,$\widehat{AD}$=$\frac{π}{2}$,点B在射线AD上,若BC∥OA,判断直线CD与⊙O的位置关系,并说明理由.
如图,点A、点D在⊙O上,0A=1,$\widehat{AD}$=$\frac{π}{2}$,点B在射线AD上,若BC∥OA,判断直线CD与⊙O的位置关系,并说明理由.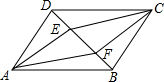 在?ABCD中,BD是对角线,AE⊥BD,CF⊥BD,E、F为垂足,求证:四边形AECF是平行四边形.
在?ABCD中,BD是对角线,AE⊥BD,CF⊥BD,E、F为垂足,求证:四边形AECF是平行四边形.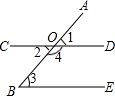 看图填理由:
看图填理由: