题目内容
13.已知点A(m+2,3)和点B(m-1,2m-4),且AB∥x轴.(1)求m的值;
(2)求AB的长.
分析 (1)由AB∥x轴,可以知道A、B两点纵坐标相等,解关于m的一元一次方程,求出m的值;
(2)由(1)求得m值求出点A、B坐标,由A、B两点横坐标相减的绝对值即为AB的长度.
解答 解:(1)∵A(m+2,3)和点B(m-1,2m-4),且AB∥x轴,
∴2m-4=3,
∴m=$\frac{7}{2}$.
(2)由(1)得:m=$\frac{7}{2}$,
∴m+2=$\frac{11}{2}$,m-1=$\frac{5}{2}$,2m-4=3,
∴A($\frac{11}{2}$,3),B($\frac{5}{2}$,3),
∵$\frac{11}{2}$-$\frac{5}{2}$=3,
∴AB的长为3.
点评 题目考查了平面直角坐标系中图形性质,题目较为简单.学生在解决此类问题时一定要灵活运用点的特征.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.当x=1时,代数式ax3+bx+5的值为-9,那么,当x=-1时,代数式ax3+bx+5的值为( )
| A. | 19 | B. | -9 | C. | 9 | D. | 1 |
4.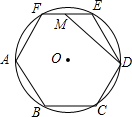 如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
 如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 1 |
18.某市因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型挖掘机 | 120 | 80 |
| 乙型挖掘机 | 100 | 60 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
 课堂上,左老师让同学们讨论一道题:如图,已知AB=AD,∠ABC=∠ADC.求证:BC=DC.
课堂上,左老师让同学们讨论一道题:如图,已知AB=AD,∠ABC=∠ADC.求证:BC=DC. 如图,在△ABC中,∠1=∠2,∠3=∠4,∠BAC=60°,则∠DAC=20°.
如图,在△ABC中,∠1=∠2,∠3=∠4,∠BAC=60°,则∠DAC=20°.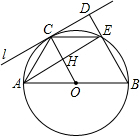 如图,⊙O的直径AB,C为圆周上一点,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E,连接EA、EC.若AB=4,AC=2,则ED的长1.
如图,⊙O的直径AB,C为圆周上一点,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E,连接EA、EC.若AB=4,AC=2,则ED的长1.