题目内容
1.先化简,再求值:$\frac{x-4}{x-3}÷$(x+3-$\frac{7}{x-3}$),其中x=-$\frac{1}{2}$.分析 首先对括号内的式子进行通分相加,把除法转化为乘法,然后进行乘法计算即可化简,然后代入数值计算即可.
解答 解:原式=$\frac{x-4}{x-3}$÷$\frac{(x+3)(x-3)-7}{x-3}$
=$\frac{x-4}{x-3}$÷$\frac{{x}^{2}-16}{x-3}$
=$\frac{x-4}{x-3}$•$\frac{x-3}{(x+4)(x-4)}$
=$\frac{1}{x+4}$,
当x=-$\frac{1}{2}$时,原式=$\frac{1}{-\frac{1}{2}+4}$=$\frac{2}{7}$.
点评 本题考查了分式的化简求值,解这类题的关键是利用分解因式的方法化简分式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )


| A. | O→B→A→O | B. | O→A→C→O | C. | O→C→D→O | D. | O→B→D→O |
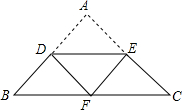 如图,在△ABC中,AB=AC,DE∥BC,现将△ABC沿DE进行折叠,使点A恰好落在BC上的点F处,则△FDE与△ABC的周长比为1:2.
如图,在△ABC中,AB=AC,DE∥BC,现将△ABC沿DE进行折叠,使点A恰好落在BC上的点F处,则△FDE与△ABC的周长比为1:2.
 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.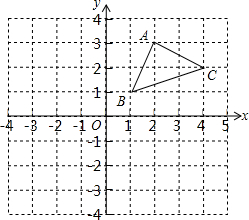 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).