题目内容
3.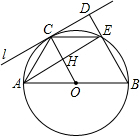 如图,⊙O的直径AB,C为圆周上一点,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E,连接EA、EC.若AB=4,AC=2,则ED的长1.
如图,⊙O的直径AB,C为圆周上一点,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E,连接EA、EC.若AB=4,AC=2,则ED的长1.
分析 根据切线的性质得到OC⊥l,而BD⊥l,则OC∥BD,根据圆周角定理得到∠AEB=90°,即BD⊥AE,所以OC⊥AE,根据垂径定理得到CA弧=CE弧,所以CA=CE;根据圆周角定理得到∠ACB=90°,根据圆内接四边形的性质得到∠DEC=∠CAB,则△CDE∽△BCA,然后根据相似比DE:AC=CE:AB可计算出DE.
解答 解:∵l与⊙O的相切于C点,
∴OC⊥l,
∵BD⊥l,
∴OC∥BD,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴BD⊥AE,
∴OC⊥AE,
∴CA弧=CE弧,
∴CA=CE;
连结BC,如图,
∵∠DEC=∠CAB,
∴△CDE∽△BCA,
∴DE:AC=CE:AB,
而CE=CA=2,
∴DE:2=2:4,
∴ED=1.
故答案为:1.
点评 本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了圆周角定理、垂径定理以及三角形相似的判定与性质.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
18.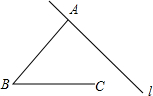 如图所示的平面图形中,下列说法错误的是( )
如图所示的平面图形中,下列说法错误的是( )
 如图所示的平面图形中,下列说法错误的是( )
如图所示的平面图形中,下列说法错误的是( )| A. | 直线l经过点A | B. | 射线BC不与直线l相交 | ||
| C. | 点B在直线l外 | D. | 点A到点B的距离是线段AB的长度 |
5.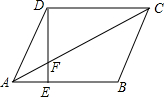 如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )
如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )
 如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )
如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )| A. | 12cm2 | B. | 24cm2 | C. | 36cm2 | D. | 48cm2 |
 如图,将一根长为20cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,筷子露在杯子外面的长度为7cm.
如图,将一根长为20cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,筷子露在杯子外面的长度为7cm.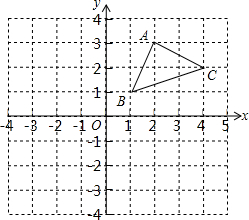 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).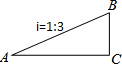 如图,小明沿坡度i=1:3的一段斜坡从A向上爬行到B,已知AB=30米,则小明在水平方向上前进了9$\sqrt{10}$米.
如图,小明沿坡度i=1:3的一段斜坡从A向上爬行到B,已知AB=30米,则小明在水平方向上前进了9$\sqrt{10}$米.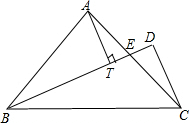 如图,等腰Rt△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC交AC于E,过C作CD⊥BE于D点,写出AT、CD与BD之间的数量关系并证明.
如图,等腰Rt△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC交AC于E,过C作CD⊥BE于D点,写出AT、CD与BD之间的数量关系并证明.