题目内容
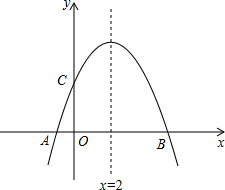 如图,在平面直角坐标系xOy中,一次函数y=
如图,在平面直角坐标系xOy中,一次函数y=| 5 |
| 4 |
(1)求m的值及抛物线C1:y=ax2+bx+c(a≠0)的函数表达式.
(2)设点D(0,
| 25 |
| 12 |
| 1 |
| M1F |
| 1 |
| M2F |
(3)将抛物线C1作适当平移,得到抛物线C2:y2=-
| 1 |
| 4 |
考点:二次函数综合题,一元二次方程的应用,两点间的距离公式
专题:压轴题
分析:(1)只需将A点坐标代入一次函数关系式即可求出m值,利用待定系数法和二次函数的图象与性质列出关于a、b、c的方程组求出a、b、c的值就可求出二次函数关系式;
(2)先运用轴对称的性质找到点F的坐标,再运用一元二次方程根与系数的关系及平面直角坐标系中两点之间的距离公式求出M1M2、M1F、M2F,证出M1F•M2F=M1M2,最后可求
+
=1;
(3)设y2与y=-x的两交点的横坐标分别为x0,x0,因为抛物线C2:y2=-
(x-h)2可以看成由y=-
x2左右平移得到,观察图象可知,随着图象向右移,x0,x0的值不断增大,所以当1<x≤m,y2≥-x恒成立时,m最大值在x0处取得,根据题意列出方程求出x0,即可求解.
(2)先运用轴对称的性质找到点F的坐标,再运用一元二次方程根与系数的关系及平面直角坐标系中两点之间的距离公式求出M1M2、M1F、M2F,证出M1F•M2F=M1M2,最后可求
| 1 |
| M1F |
| 1 |
| M2F |
(3)设y2与y=-x的两交点的横坐标分别为x0,x0,因为抛物线C2:y2=-
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)∵一次函数y=
x+m的图象与x轴交于A(-1,0)
∴0=-
+m
∴m=
.
∴一次函数的解析式为y=
x+
.
∴点C的坐标为(0,
).
∵y=ax2+bx+c(a≠0)经过A、C两点且对称轴是x=2,
∴
,解得
∴y=-
x2+x+
.
∴m的值为
,抛物线C1的函数表达式为y=-
x2+x+
.
(2)要使△ADF的周长取得最小,只需AF+DF最小
连接BD交x=2于点F,因为点B与点A关于x=2对称,
根据轴对称性质以及两点之间线段最短,可知此时AF+DF最小.
令y=-
x2+x+
中的y=0,则x=-1或5
∴B(5,0)
∵D(0,
)
∴直线BD解析式为y=-
x+
,
∴F(2,
).
令过F(2,
)的直线M1M2解析式为y=kx+b1,
则
=2k+b1,∴b1=
-2k
则直线M1M2的解析式为y=kx+
-2k.
解法一:
由
得x2-(4-4k)x-8k=0
∴x1+x2=4-4k,x1x2=-8k
∵y1=kx1+
-2k,y2=kx2+
-2k
∴y1-y2=k(x1-x2)
∴M1M2=
=
=
=
=
=4(1+k2)
M1F=
=
=
同理M2F=
∴M1F•M2F=(1+k2)
=(1+k2)
=(1+k2)
=4(1+k2)=M1M2
∴
+
=
=
=1;
解法二:
∵y=-
x2+x+
=-
(x-2)2+
,
∴(x-2)2=9-4y
设M1(x1,y1),则有(x1-2)2=9-4y1.
∴M1F=
=
=
-y1;
设M2(x2,y2),同理可求得:M2F=
-y2.
∴
+
=
=
=
①.
直线M1M2的解析式为y=kx+
-2k,即:y-
=k(x-2).
联立y-
=k(x-2)与抛物线(x-2)2=9-4y,得:
y2+(4k2-
)y+
-9k2=0,
∴y1+y2=
-4k2,y1y2=
-9k2,代入①式,得:
+
=
=1.
(3)设y2与y=-x的两交点的横坐标分别为x0,x0′,
∵抛物线C2:y2=-
(x-h)2可以看成由y=-
x2左右平移得到,观察图象可知,随着图象向右移,x0,x0′的值不断增大
∴当1<x≤m,y2≥-x恒成立时,m最大值在x0′处取得
∴当x0=1时,对应的x0′即为m的最大值
将x0=1代入y2=-
(x-h)2=-x得(1-h)2=4,
∴h=3或-1(舍)
将h=3代入y2=-
(x-h)2=-x有
-
(x-3)2=-x
∴x0=1,x0′=9.
∴m的最大值为9.
| 5 |
| 4 |
∴0=-
| 5 |
| 4 |
∴m=
| 5 |
| 4 |
∴一次函数的解析式为y=
| 5 |
| 4 |
| 5 |
| 4 |
∴点C的坐标为(0,
| 5 |
| 4 |
∵y=ax2+bx+c(a≠0)经过A、C两点且对称轴是x=2,
∴
|
|
∴y=-
| 1 |
| 4 |
| 5 |
| 4 |
∴m的值为
| 5 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
(2)要使△ADF的周长取得最小,只需AF+DF最小
连接BD交x=2于点F,因为点B与点A关于x=2对称,
根据轴对称性质以及两点之间线段最短,可知此时AF+DF最小.
令y=-
| 1 |
| 4 |
| 5 |
| 4 |
∴B(5,0)
∵D(0,
| 25 |
| 12 |
∴直线BD解析式为y=-
| 5 |
| 12 |
| 25 |
| 12 |
∴F(2,
| 5 |
| 4 |
令过F(2,
| 5 |
| 4 |
则
| 5 |
| 4 |
| 5 |
| 4 |
则直线M1M2的解析式为y=kx+
| 5 |
| 4 |
解法一:
由
|
得x2-(4-4k)x-8k=0
∴x1+x2=4-4k,x1x2=-8k
∵y1=kx1+
| 5 |
| 4 |
| 5 |
| 4 |
∴y1-y2=k(x1-x2)
∴M1M2=
| (x1-x2)2+(y1-y2)2 |
=
| (x1-x2)2+k2(x1-x2)2 |
=
| 1+k2 |
| (x1-x2)2 |
=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
| (4-4k)2+32k |
=4(1+k2)
M1F=
(x1-2)2+(y1-
|
=
(x1-2)2+(kx1+
|
=
| 1+k2 |
| (x1-2)2 |
同理M2F=
| 1+k2 |
| (x2-2)2 |
∴M1F•M2F=(1+k2)
| (x1-2)2(x2-2)2 |
=(1+k2)
| [x1x2-2(x1+x2)+4]2 |
=(1+k2)
| [-8k-2(4-4k)+4]2 |
=4(1+k2)=M1M2
∴
| 1 |
| M1F |
| 1 |
| M2F |
| M1F+M2F |
| M1F•M2F |
=
| M1M2 |
| M1F•M2F |
解法二:
∵y=-
| 1 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
∴(x-2)2=9-4y
设M1(x1,y1),则有(x1-2)2=9-4y1.
∴M1F=
(x1-2)2+(
|
(
|
| 13 |
| 4 |
设M2(x2,y2),同理可求得:M2F=
| 13 |
| 4 |
∴
| 1 |
| M1F |
| 1 |
| M2F |
| M1F+M2F |
| M1F•M2F |
(
| ||||
(
|
| ||||
|
直线M1M2的解析式为y=kx+
| 5 |
| 4 |
| 5 |
| 4 |
联立y-
| 5 |
| 4 |
y2+(4k2-
| 5 |
| 2 |
| 25 |
| 16 |
∴y1+y2=
| 5 |
| 2 |
| 25 |
| 16 |
| 1 |
| M1F |
| 1 |
| M2F |
| 4k2+4 |
| 4k2+4 |
(3)设y2与y=-x的两交点的横坐标分别为x0,x0′,
∵抛物线C2:y2=-
| 1 |
| 4 |
| 1 |
| 4 |
∴当1<x≤m,y2≥-x恒成立时,m最大值在x0′处取得
∴当x0=1时,对应的x0′即为m的最大值
将x0=1代入y2=-
| 1 |
| 4 |
∴h=3或-1(舍)
将h=3代入y2=-
| 1 |
| 4 |
-
| 1 |
| 4 |
∴x0=1,x0′=9.
∴m的最大值为9.
点评:本题主要考查运用待定系数法求函数解析式、一元二次方程根与系数的关系及平面直角坐标系中两点距离公式的综合运用,对计算要求较高.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图,在梯形ABCD中,AB∥CD,若AB=8,CD=x,梯形的高是6.
如图,在梯形ABCD中,AB∥CD,若AB=8,CD=x,梯形的高是6. 今年“六一”儿童节当天,小兵一家三口自驾车去离家220千米的“儿童乐园”游玩,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
今年“六一”儿童节当天,小兵一家三口自驾车去离家220千米的“儿童乐园”游玩,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象. 如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.

 如图,矩形ABCD中,AB=2,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=
如图,矩形ABCD中,AB=2,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD= 如图,AB∥CD,AD和BC相交于点O,∠A=20°,∠COD=100°,则∠C的度数是
如图,AB∥CD,AD和BC相交于点O,∠A=20°,∠COD=100°,则∠C的度数是