题目内容
 如图,矩形ABCD中,AB=2,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=
如图,矩形ABCD中,AB=2,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=考点:翻折变换(折叠问题)
专题:几何图形问题
分析:连接EF,则可证明△EA′F≌△EDF,从而根据BF=BA′+A′F,得出BF的长,在Rt△BCF中,利用勾股定理可求出BC,即得AD的长度.
解答:解:连接EF,
∵点E、点F是AD、DC的中点,
∴AE=ED,CF=DF=
CD=
AB=1,
由折叠的性质可得AE=A′E,
∴A′E=DE,
在Rt△EA′F和Rt△EDF中,
,
∴Rt△EA′F≌Rt△EDF(HL),
∴A′F=DF=1,
∴BF=BA′+A′F=AB+DF=2+1=3,
在Rt△BCF中,
BC=
=
=2
.
∴AD=BC=2
.
故答案为:2
.
∵点E、点F是AD、DC的中点,
∴AE=ED,CF=DF=
| 1 |
| 2 |
| 1 |
| 2 |
由折叠的性质可得AE=A′E,

∴A′E=DE,
在Rt△EA′F和Rt△EDF中,
|
∴Rt△EA′F≌Rt△EDF(HL),
∴A′F=DF=1,
∴BF=BA′+A′F=AB+DF=2+1=3,
在Rt△BCF中,
BC=
| BF2-CF2 |
| 8 |
| 2 |
∴AD=BC=2
| 2 |
故答案为:2
| 2 |
点评:本题考查了翻折变换的知识,解答本题的关键是连接EF,证明Rt△EA′F≌Rt△EDF,得出BF的长,注意掌握勾股定理的表达式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
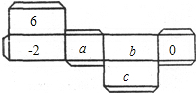 如图是一个长方体墨水瓶纸盒的表面展开图,已知纸盒中相对两个面上的数互为相反数.
如图是一个长方体墨水瓶纸盒的表面展开图,已知纸盒中相对两个面上的数互为相反数. 画出函数y=-x+1的图象,结合图象,回答下列问题.
画出函数y=-x+1的图象,结合图象,回答下列问题. 如图,△ABC中,AD是高,BE平分∠ABC.
如图,△ABC中,AD是高,BE平分∠ABC.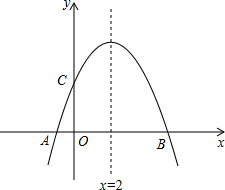 如图,在平面直角坐标系xOy中,一次函数y=
如图,在平面直角坐标系xOy中,一次函数y= 如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,且BC∥OD,若AB=4,OD=6,则BC的长等于
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,且BC∥OD,若AB=4,OD=6,则BC的长等于 如图,AE∥BF,AC平分∠BAE,交BF于点C,若∠ACF=130°,则∠B的度数为
如图,AE∥BF,AC平分∠BAE,交BF于点C,若∠ACF=130°,则∠B的度数为