题目内容
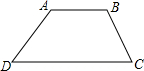如图，在梯形ABCD中，AB∥CD，若AB=8，CD=x，梯形的高是6．（1）求梯形ABCD的面积y与x下底之间的关系式；
（2）当x增加l时，y如何变化．
考点：函数关系式
专题：
分析：（1）根据梯形面积公式列出函数关系式即可；
（2）计算出x=a+1与x=a时y的值，再相减即可．
（2）计算出x=a+1与x=a时y的值，再相减即可．
解答：解：（1）y=
（8+x）•6，即y=3x+24
故所求的关系式为y=3x+24；
（2）当x=a时，y=3a+24，
当x=a+1时，y=3（a+1）+24=3a+27，
3a+27-（3a+24）=3，
故当x增加l时，y增加3．
| 1 |
| 2 |
故所求的关系式为y=3x+24；
（2）当x=a时，y=3a+24，
当x=a+1时，y=3（a+1）+24=3a+27，
3a+27-（3a+24）=3，
故当x增加l时，y增加3．
点评：本题考查了一次函数的应用．关键是根据梯形面积公式列出一次函数关系式，利用函数关系式解答问题．
练习册系列答案
相关题目
有理数a、b、c的位置如图，下面的判断正确的是（ ）
| A、abc＜0 |
| B、a-b＞0 |
| C、|c|＜|b| |
| D、c-a＞0 |
函数y=
+3中，自变量x的取值范围是（ ）
| 1 | ||
|
| A、x＞5 | B、x≥-5 |
| C、x≤-5 | D、x＞-5 |
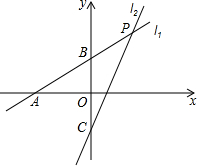如图，直线l1：y=k1+b1（k≠0）分别与x轴、y轴相交于点A（-5，0）和点B（0，2），直线l2：y=2x+b2 与直线l1相交于点P、与y轴相交于点C，已知点P的纵坐标为3．
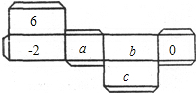如图是一个长方体墨水瓶纸盒的表面展开图，已知纸盒中相对两个面上的数互为相反数．
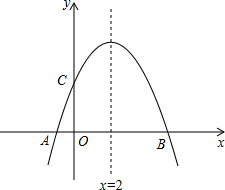如图，在平面直角坐标系xOy中，一次函数y=