题目内容
13．已知在平行四边形ABCD中，AB=15、AC=13，BC边上的高是12，则平行四边形ABCD的周长等于58或38．分析 首先根据题意画出图形，然后分别从高在平行四边形内部与外部，去分析求解即可求得答案．
解答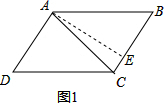 
解：，∵AB=15、AC=13，BC边上的高是12，
即AE=12，
∴在Rt△ABE中，BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=9，
在Rt△ACE中，CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=5，
如图1，BC=BE+CE=14，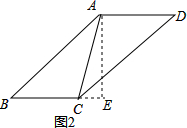
∴平行四边形ABCD的周长为：2（AB+BC）=58，
如图2，BC=BE-CE=4，
∴平行四边形ABCD的周长为：2（AB+BC）=38，
综上可得：平行四边形ABCD的周长等于：58或38．
故答案为：58或38．
点评 此题考查了平行四边形的性质以及勾股定理．注意掌握分类讨论思想的应用是解此题的关键．
练习册系列答案
相关题目
11．
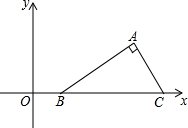如图，在平面直角坐标系中Rt△ABC的斜边BC在x轴上，点B坐标为（1，0），AC=2，∠ABC=30°，把Rt△ABC先绕B点顺时针旋转180°，然后再向下平移2个单位，则A点的对应点A′的坐标为（ ）
如图，在平面直角坐标系中Rt△ABC的斜边BC在x轴上，点B坐标为（1，0），AC=2，∠ABC=30°，把Rt△ABC先绕B点顺时针旋转180°，然后再向下平移2个单位，则A点的对应点A′的坐标为（ ）| A． | （-4，-2-$\sqrt{3}$） | B． | （-4，-2+$\sqrt{3}$） | C． | （-2，-2+$\sqrt{3}$） | D． | （-2，-2-$\sqrt{3}$） |
矩形ABCD中，AC是对角线，AB=$\sqrt{3}$，将△ABC绕点C顺时针旋转60°，点B恰好落在AD边上的点E处，点A经过的路径是$\widehat{AF}$，则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$．（结果保留π）．
1．x=$\sqrt{3}$+1，y=$\sqrt{3}$-1，则（1+$\frac{1}{y}$）（1-$\frac{1}{x}$）=（ ）
| A． | $4\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $2\sqrt{3}$ | D． | $\frac{3}{2}$ |
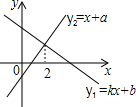一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k＜0；②a＞0；③当x＜3时，y1＜y2中，正确的序号是①．
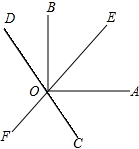如图，直线EF，CD相交于点O，OA⊥OB，且OC平分∠AOF．
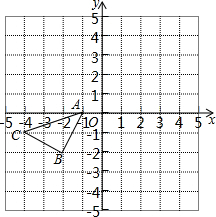如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：
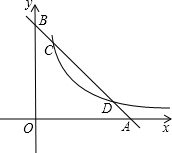已知：一次函数y=-x+b的图象与x轴、y轴的交点分别为A、B与反比例函数$y=\frac{5}{x}（x＞0）$的图象交于点C、D，且$\frac{BD}{BA}=\frac{2}{3}$．