题目内容
1．x=$\sqrt{3}$+1，y=$\sqrt{3}$-1，则（1+$\frac{1}{y}$）（1-$\frac{1}{x}$）=（ ）| A． | $4\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $2\sqrt{3}$ | D． | $\frac{3}{2}$ |
分析 根据x=$\sqrt{3}$+1，y=$\sqrt{3}$-1，可以求得（1+$\frac{1}{y}$）（1-$\frac{1}{x}$）的值，本题得以解决．
解答 解：∵x=$\sqrt{3}$+1，y=$\sqrt{3}$-1，
∴（1+$\frac{1}{y}$）（1-$\frac{1}{x}$）
=（1+$\frac{1}{\sqrt{3}-1}$）（1-$\frac{1}{\sqrt{3}+1}$）
=（1+$\frac{\sqrt{3}+1}{2}$）（1-$\frac{\sqrt{3}-1}{2}$）
=1-$\frac{\sqrt{3}-1}{2}$+$\frac{\sqrt{3}+1}{2}$-$\frac{1}{2}$
=$\frac{3}{2}$，
故选D．
点评 本题考查分式的混合运算，解题的关键是明确分式的混合运算的计算法，计算时要仔细认真．
练习册系列答案
阅读快车系列答案
相关题目
如图，从圆O外的两点C和D分别引圆的两条切线DA，DC，CB，切点分别是A、E和B，AB是圆O的直径，连接OC、OD，延长DO交CB的延长线于点F，给出如下结论：①AD+BC=CD；②OD2=DE•CD；③CO=DF；④△AOD∽△BCO，其中正确的是①②④．（把所有正确的序号都填在横线上）．
10．为了防控甲型H1N1流感，某校积极进行校园的环境消毒，为此购买了甲、乙两种消毒液，现已知过去两次购买这两种消毒液的瓶数和总费用如表所示：
（1）求每瓶甲种消毒和每瓶乙种消毒液各多少元？
（2）现在学校决定购买甲乙两种消毒液共300瓶，要求甲乙两种的数量都不少于100瓶，并且甲的数量不少于乙数量的$\frac{3}{2}$，请你帮助学校计算购买时最低费用为多少？
| 甲种消毒液（瓶） | 乙种消毒液（瓶） | 总费用（元） | |
| 第一次 | 40 | 60 | 660 |
| 第二次 | 80 | 30 | 690 |
（2）现在学校决定购买甲乙两种消毒液共300瓶，要求甲乙两种的数量都不少于100瓶，并且甲的数量不少于乙数量的$\frac{3}{2}$，请你帮助学校计算购买时最低费用为多少？
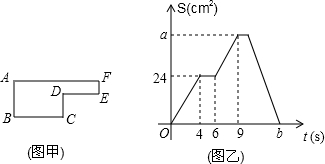
如图，平行四边形中，AE⊥BC于E，AF⊥CD于F．