题目内容
11.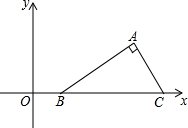 如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )| A. | (-4,-2-$\sqrt{3}$) | B. | (-4,-2+$\sqrt{3}$) | C. | (-2,-2+$\sqrt{3}$) | D. | (-2,-2-$\sqrt{3}$) |
分析 首先根据直角三角形的性质和勾股定理可得BC,AB,利用直角三角形的面积可得AD,再利用射影定理易得BD,可得点A的坐标,根据旋转的性质易得A1的坐标,再利用平移的性质可得结果.
解答 解:作AD⊥BC,并作出把Rt△ABC先绕B点顺时针旋转180°后所得△A1BC1,如图所示,
∵AC=2,∠ABC=30°,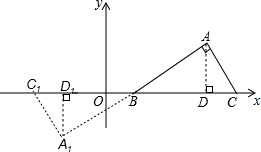
∴BC=4
∴AB=2$\sqrt{3}$,
∴AD=$\frac{AB•AC}{BC}$=$\frac{2\sqrt{3}×2}{4}$=$\sqrt{3}$,
∴BD=$\frac{A{B}^{2}}{BC}$=$\frac{{(2\sqrt{3})}^{2}}{4}$=3,
∵点B坐标为(1,0),
∴A点的坐标为(4,$\sqrt{3}$),
∵BD=3,
∴BD1=3,
∴D1坐标为(-2,0)
∴A1坐标为(-2,-$\sqrt{3}$),
∵再向下平移2个单位,
∴A′的坐标为(-2,-$\sqrt{3}$-2),
故选D.
点评 本题主要考查了直角三角形的性质,勾股定理,旋转的性质和平移的性质,作出图形利用旋转的性质和平移的性质是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知点(x1,y1)和(x2,y2)都在函数y=-2x+4的图象上.则下列结论正确的是( )
| A. | 若y1<y2,则x1<x2 | |
| B. | 若y1-y2=2,则x1-x2=-1 | |
| C. | 可由直线y=2x向上平移4个单位得到 | |
| D. | 与坐标系围成的三角形面积为8 |
3.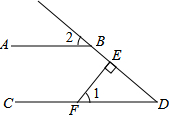 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
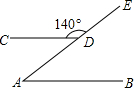 如图,点D在射线AE上,AB∥CD,∠CDE=140°,求∠A的度数.
如图,点D在射线AE上,AB∥CD,∠CDE=140°,求∠A的度数.