题目内容
18.函数y=2x和y=ax+4的图象相交于点A(m,3),则方程2x=ax+4的解为x=1.5.分析 可先求得A点坐标,再结合函数图象可知方程的解即为两函数图象的交点横坐标,可求得方程的解.
解答 解:∵A点在直线y=2x上,
∴3=2m,解得m=1.5,
∴A点坐标为(1.5,3),
∵y=2x,y=ax+4,
∴方程2x=ax+4的解即为两函数图象的交点横坐标,
∴方程2x=ax+4的解为x=1.5,
故答案为:x=1.5.
点评 本题主要考查函数图象交点的意义,掌握函数图象的交点即为对应方程组的解是解题的关键.

练习册系列答案
相关题目
10.为了防控甲型H1N1流感,某校积极进行校园的环境消毒,为此购买了甲、乙两种消毒液,现已知过去两次购买这两种消毒液的瓶数和总费用如表所示:
(1)求每瓶甲种消毒和每瓶乙种消毒液各多少元?
(2)现在学校决定购买甲乙两种消毒液共300瓶,要求甲乙两种的数量都不少于100瓶,并且甲的数量不少于乙数量的$\frac{3}{2}$,请你帮助学校计算购买时最低费用为多少?
| 甲种消毒液(瓶) | 乙种消毒液(瓶) | 总费用(元) | |
| 第一次 | 40 | 60 | 660 |
| 第二次 | 80 | 30 | 690 |
(2)现在学校决定购买甲乙两种消毒液共300瓶,要求甲乙两种的数量都不少于100瓶,并且甲的数量不少于乙数量的$\frac{3}{2}$,请你帮助学校计算购买时最低费用为多少?
8.一个手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部、B型手机y部,三款手机的进价和预售价如表:
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
| 手机型号 | A型 | B型 | C型 |
| 进价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
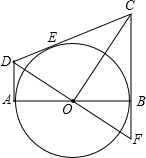 如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).
如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).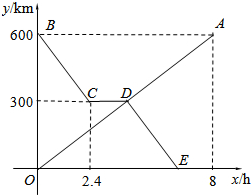 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系. 如图1所示的是一个长方形纸带,∠DEF=25°,将纸带沿EF折叠成图2,则图2中的∠BGE的度数是50°.
如图1所示的是一个长方形纸带,∠DEF=25°,将纸带沿EF折叠成图2,则图2中的∠BGE的度数是50°.